IJCRR

IJCRR - 8(6), March, 2016

Pages: 40-46

Date of Publication: 22-Mar-2016

PROPAGATION OF THE SHOCK WAVES IN THE EXPONENTIALLY DECREASING ATMOSPHERE

Author: Rajan Singh, Mukesh Chandra, Anand kumar

Category: Healthcare

Abstract:The purpose of the present paper is to study propagation of the shock waves and the flow parameters in the exponentially decreasing atmosphere. Plane shock waves as it propagates vertically upward in the static atmosphere of the earth are also studied. The variation of Mach number and the velocity of the shock waves are obtained analytically by using Whitham's Rule. It is found that shock velocity increases as the shock wave propagates in the atmosphere with decreasing density normal to plane of the shock front

Keywords: Shock wave, Pressure, Density, Velocity, Mach number, Propagation, Adiabatic and isothermal atmosphere

Full Text:

1. INTRODUCTION Bhatnagar and Sachdev [1] have obtained a relation between the density, pressure and Mach number by using Whitham’s Rule to the propagation of the shock waves in the nonhomogeneous medium. Kopal and Carrus [2], Hardy and Grover [3] have been studied the problem of propagation of the shock waves in a non-uniform medium with various density distributions and found the behavior of the fluid flow in the presence of the shock waves. Hayes [4] investigated the vorticity jump across a gas dynamics discontinuity by considering the radiative heat transfer into account and concluded that for an optically thin gas, vorticity is unaffected in pseudo-stationary flows. Kanwal [5, 6] employed the theory of generalized functions and differential geometry to study the propagation and deformation of wave front in stationary three dimensional gas flows.

With minor changes the experimental data for temperature distribution given by Mitra [8,9] has been used .So the aim of the present paper is to see how the shock velocity varies in the absence of any body force as the shock waves propagate in the atmosphere, in which the density is decreasing exponentially, Whitham’s Rule [10] is applied to find and approximate analytic relation for the Mach number and the shock velocity. In this paper, we have studied the problem of propagation of the shock waves in the earth’s atmosphere and also used the Whitham’s rule. The experimental data for temperature distribution given by Mitra [8] has been used for minor changes.

RESEARCH METHODOLOGY The following Research Methodology is adopted for the proposed Research paper: • Identification of the problem • Collection and study of related literature • Mathematical formulation of the problem • Analysis and numerical solution of the mathematical model • Interpretation of results • Conclusion.

2. FORMULATION OF THE PROBLEM Let us assume that a gaseous medium, in which the pressure, the temperature and the density vary along a fixed direction. Let us consider that the X -axis of the medium be taken along this direction and the distance measured along this axis be denoted by x. So that the thermo dynamical parameters. In the direction normal to the X -axis are constant. Let the pressure P0 the temperature T0 and the density p0 at a distance x measured from a fixed plane denoted by x = o and Ps , Ts and

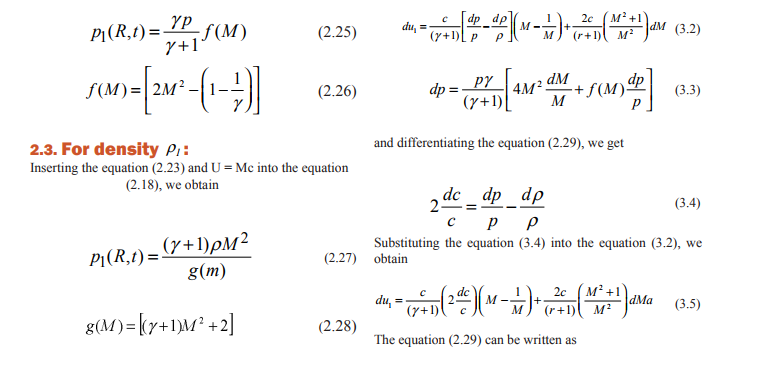
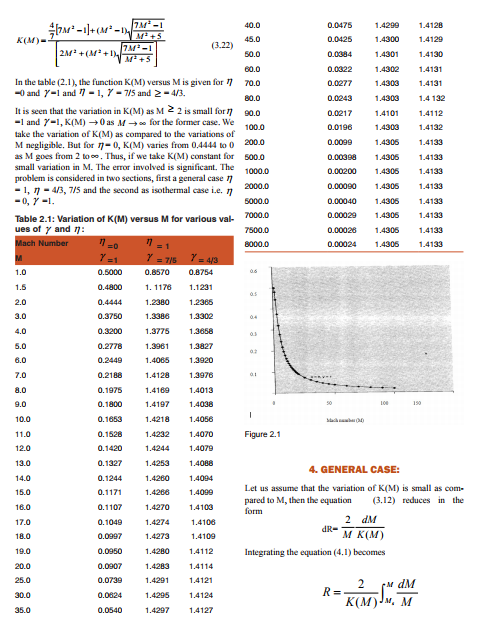
CONCLUSION In this paper, if is very useful discussed the Plane shock waves as it propagates vertically upward in the static atmosphere of the earth studied. It is found that shock velocity increases as the shock wave propagates in the atmosphere with decreasing density normal to plane of the shock front.

ACKNOWLEDGEMENT Authors acknowledge the immense help received from the scholars whose articles are cited and included in the manuscript. The authors are also grateful to authors / editors / publishers of all those articles, journals and books from where the literature for this article has been reviewed and discussed. Authors are grateful to IJCRR editorial board members and reviewers for their useful comments that lead the improvement of the manuscript.

References:

1. Bhatnagar, P.L., Sahdev, P.L., Nuovo Cimento, 44, (1966), pp. 5-15.

2. Carrus, P.A., Fox, P.A., Kopal, Z., Hoas, F. , Ap. J., (1951), pp.113.

3. Grover R. and Hardy, J.W., App. J. (1966), 143.193,496,48.

4. Hayes, W.O. The vorticity jump across a gas dynamics discontinuity. J. Fluid Mech, 2(1957), p.597-600.

5. Kanwal, R.P. Propagation of curved shocks in pseudo [1] stationary three dimensional gas flows. Illinois; J.Math, 2( 1958), p.129-136.

6. Kanwal, R.P. Flows behind shock waves in conducting gases, Proc. Roy. Soc., 257( 1960), p.263-268.

7. Kolobkov, N., Our Atmospherics Ocean Foreign Language Publishing, House Moscow,(1960), p.41.

8. Mitra, S. K.,Upper atmosphere, Asiatic Society, Calcutta (1952).

9. Mishra, R.S., Determination of jump conditions across a 3D shock in conducting fluids.

10. Whithan, G.B , On the propagation of the shock waves through regions of non-uniform area or Flow , J. Fluid, Mech (1956), p.337-360.