IJCRR

IJCRR - 9(7), April, 2017

Pages: 01-04

Date of Publication: 11-Apr-2017

An Overview of Recent Developments of Fuzzy Divergence Measures and their Generalizations

Author: Anshu Ohlan

Category: General Sciences

Abstract:Aim: The aim of the paper is to present an overview of recent developments in fuzzy divergence measures.
Methodology: We analysis some of well-known notions and the concepts associated with fuzzy set theory with an axiomatic definition of fuzzy divergence measure.
Results: Fuzzy divergence measures and their generalizations existing in the literature are summarized briefly.
Conclusion: The reviewed divergence measures and their generalizations are useful for further development of measures of divergence and appropriate to deal with different areas.

Keywords: Fuzzy Sets, Fuzzy Measure of Information, Fuzzy Divergence Measures

Full Text:

INTRODUCTION

In 1965, as a generalization of classical (crisp) set theory, Zadeh [1] first proposed the concept of fuzzy set theory. It was found to be suitable in dealing with many fields like pattern recognition, image processing, speech recognition, bioinformatics, fuzzy aircraft control, feature selection, decision making, etc. Over the last six decades, the study on fuzzy set (FS) theory and its application to different area has been extended evenly by the researchers. Afterwards, in 1965, Zadeh [2] introduced the notion of fuzzy entropy as a measure of uncertainty. In 1972, De Luca and Termini [3] presented an axiomatic composition of fuzzy entropy corresponding to the probabilistic entropy measure of Shannon [4]. For determining  the difference between the two FSs divergence measure is a significant tool among the most exciting measures in FSs theory. The concept of fuzzy divergence measure is itself one of the generalization of fuzzy information measure. Analogous to Kullback and Leibler [5] measure of divergence, Bhandari and Pal [6] introduced the fuzzy divergence measure. Thereafter literature on fuzzy measures of information, divergence and their generalizations are considerably extended by the different researchers [7-25] in the past decades.

Briefly motivated by the study of the literature on measures of fuzzy information and their generalization in the paper Methodology section introduce some well-known concepts, and the notation related to fuzzy set theory, axiomatic definitions of fuzzy information measure, fuzzy divergence measure etc. In the results section, we  provide an overview of recent developments in fuzzy divergence measures and their generalizations. An essential analysis of the existing  measures of divergence is presented in the discussion section. The final section concludes the paper.

METHODOLOGY

We now introduce some of well-known notions and the concepts associated with fuzzy set theory with an axiomatic definition of fuzzy divergence measure.

Zadeh [1] defined a fuzzy set (FS) on a universe of discourse U having the membership function 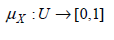   as follows:

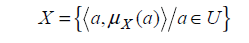
The membership value 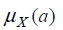 describes the degree of the belongingness of in X.  When is valued in {0, 1}, it is the characteristic function of a crisp (i.e., non-fuzzy) set.

The measure of difference between two fuzzy sets is called the fuzzy divergence measure.

Bhandari and Pal [6] initiated the measure of fuzzy divergence corresponding to divergence measure of Kullback and Leibler [5], as

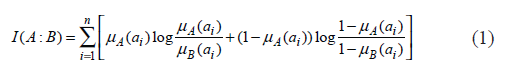
satisfying the conditions:

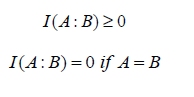
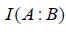is a convex function of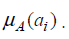

Bhandari and Pal [6] also defined the fuzzy symmetric divergence measure:

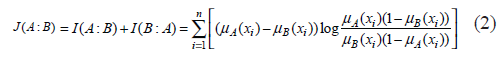
A general study of the axiomatic definition of a divergence measure for fuzzy sets was also presented in Bouchon-Meunier et al. [26]. As a significant content in fuzzy mathematics, the research on divergence measures between fuzzy sets has received more attention. In recent years, some definitions of generalized measures of fuzzy divergence have been proposed.

Afterwards, Shang and Jiang [27] provided a modified version of the fuzzy divergence measure of Bhandari and Pal [6] with the novel idea of Lin [28] and defined as

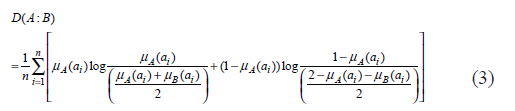
Fan and Xie [29] proposed the fuzzy information of discrimination of  against corresponding to the exponential fuzzy entropy of Pal and Pal [30] and is given by

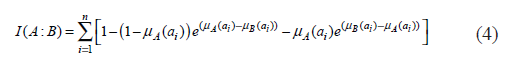
Thereafter Couso et al. [31] define that if X is a universe of discourse and F(X) is the set of all fuzzy subsets, a mapping D:F (X) x F (X)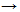 is a divergence measure between fuzzy subsets if and only if for each  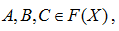the following axioms hold:

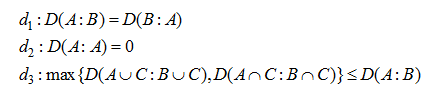
Non-negativity of 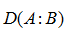  is the natural assumption. 

Montes et al. [32] studied the special classes of divergence measures and used the link between fuzzy and probabilistic uncertainty. It also studied widely the divergence measure for fuzzy sets as a particular case.

Hooda [33] presented a fuzzy divergence measure corresponding to Havada-Charvat [34] measure of divergence which is given by

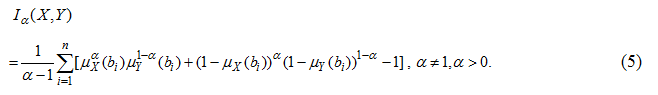
Parkash et al. [35] proposed a fuzzy divergence measure corresponding to Ferreri [36] probabilistic measure of divergence given by

  and another one given by Parkash et al. [35]  is

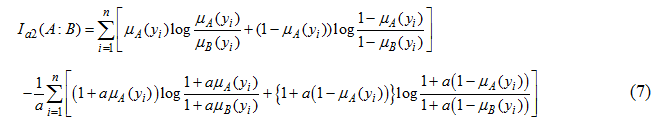
Corresponding to Renyi [36] and Sharma and Mittal [37] generalized measure of divergence Bajaj and Hooda [38] provided the generalized fuzzy divergence measure which are given by

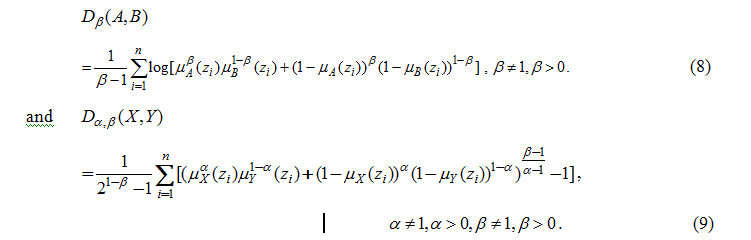
DISCUSSION

Singh and Tomar [39, 40,41,42] have defined and studied some of symmetric and non-symmetric fuzzy divergence measures analogous to probabilistic divergence measures and inequalities among them. Moreover, Singh and Tomar [43,44] presented a number of refinement of inequalities among fuzzy divergence measures. Bhatia and Singh [45] proposed three families of fuzzy divergence.

Thereafter, Hooda and Jain [46] presented a generalized fuzzy divergence measure, its ambiguity and information improvement. Further, in the recent years, fuzzy measures of information, divergence and their generalizations are considerably extended by Tomar and Ohlan [17-20 ] and Ohlan and Ohlan [9-16] and Ohlan [7,8, 21-25] and find their applications emerging in various fields like decision making (e.g., multi-criteria decision making, multi-attribute decision making), pattern recognition, medical diagnosis and suitability in linguistic variables.

CONCLUSION

In this paper we have presented a review of the fuzzy measures of divergence and their generalizations existing in the literature. It was noted that these measures of fuzzy divergence can be used for further development of generalized fuzzy divergence measures, appropriate to deal with different areas.

ACKNOWLEDGEMENT

Authors acknowledge the immense help received from the scholars whose article cited and included in references of this manuscript. The authors are also grateful to authors/editors/publishers of all those articles, journals and books from where the literature for this article has been reviewed and discussed.

Conflict of interest: Nil

Source of Funding: Nil

References:

1. L.A. Zadeh, Fuzzy sets, Information and Control 8(3) (1965), 338-353.
2. L.A. Zadeh, Probability measures of fuzzy events, Journal of Mathematical Analysis and Applications 23(1968), 421-427.
3. De Luca A. and Termini S.(1972), “A definition of non-probabilistic entropy in the setting of fuzzy set theory”, Information and Control, 20(4), 301-312.
4. Shannon C.E.(1948), “The mathematical theory of communication”, The Bell System Technical Journal, 27(3), 379-423.
5. Kullback S. and Leibler R.A.(1951), “On information and sufficiency”, The Annals of Mathematical Statistics, 22(1), 79-86.
6. Bhandari D. and Pal N.R.(1993), “Some new information measures for fuzzy sets”, Information Sciences, 67(3), 209-228.
7. Ohlan A.(2015),  “A new generalized fuzzy divergence measure and applications,” Fuzzy Information and Engineering, 7(4), 507-523.
8. Ohlan A.(2016), “Intuitionistic fuzzy exponential divergence: application in multi-attribute decision making,” Journal of Intelligent and Fuzzy Systems, 30, 1519-1530.
9. Ohlan A. and Ohlan R.(2016), “Generalizations of Fuzzy Information Measures,”  Switzerland: Springer International Publishing.
10. Ohlan A. and Ohlan R.(2016), “Fundamentals of Fuzzy Information Measures,” in Ohlan A. and Ohlan R., Generalizations of Fuzzy Information Measures, Springer International Publishing Switzerland, 1-22.
11. Ohlan A. and Ohlan R.(2016), “Parametric Generalized R-norm Fuzzy Information and Divergence Measures,” in Ohlan A. and Ohlan R., Generalizations of Fuzzy Information Measures, Springer International Publishing Switzerland, 23-52.
12. Ohlan A. and Ohlan R.(2016), “Parametric Generalized Exponential Fuzzy Divergence Measure and Strategic Decision-Making,” in Ohlan A. and Ohlan R., Generalizations of Fuzzy Information Measures, Springer International Publishing Switzerland, 53-69.
13. Ohlan A. and Ohlan R.(2016), “Sequence and Application of Inequalities Among Fuzzy Mean Difference Divergence Measures in Pattern Recognition” in Ohlan A. and Ohlan R., Generalizations of Fuzzy Information Measures, Springer International Publishing Switzerland, 71-92.
14. Ohlan A. and Ohlan R.(2016), “Applications of Generalized Fuzzy Divergence Measure Multi-criteria Decision Making and Pattern Recognition” in Ohlan A. and Ohlan R., Generalizations of Fuzzy Information Measures, Springer International Publishing Switzerland, 93-105.
15. Ohlan A. and Ohlan R.(2016), “Generalized Hellinger's Divergence Measure and Its Applications” in Ohlan A. and Ohlan R., Generalizations of Fuzzy Information Measures, Springer International Publishing Switzerland, 107-121.
16. Ohlan A. and Ohlan R.(2016), “Intuitionistic  Fuzzy  Exponential  Divergence  and  Multi-attribute Decision-Making”,  in  Ohlan  A.  and  Ohlan  R.,  Generalizations  of  Fuzzy  Information Measures, Springer International Publishing Switzerland, 123-142.   
17. Tomar V.P. and Ohlan A.(2014a), “Two new parametric generalized norm fuzzy information measures”, International Journal of Computer Applications 93(13), 22-27
18. Tomar V.P. and Ohlan A.(2014b), “Sequence of fuzzy divergence measures and inequalities”, AMO - Advanced Modeling and Optimization, 16(2), 439-452.
19. Tomar V.P. and Ohlan A.(2014c), “Sequence of inequalities among fuzzy mean difference divergence measures and their applications”, SpringerPlus, 3, 623, 1-20.
20. Tomar V.P. and Ohlan A.(2014d), “New parametric generalized exponential fuzzy divergence measure,” Journal of Uncertainty Analysis and Applications, 2(1), 1-14.
21. Ohlan A.(2016a), “Some Recent Developments on Probabilistic Information Measures,” International Journal of Innovative Research in Science, Engineering and Technology, 5(12), 20455-20460.
22. Ohlan A.(2016b), “Overview on Development of Fuzzy Information Measures,” International Journal of All Research Education and Scientific Methods (IJARESM), 4(12), 17-22.
23. Ohlan A.(2016c), “An Overview On Intuitionistic Fuzzy Similarity Measures,” International Journal of Advanced Technology in Engineering and Science, 4(11), 192-198.
24. Ohlan A.(2016d), “Generalized Exponential Fuzzy Information Measures,” International Journal of Advanced Technology in Engineering and Science, 4(12), 392-399.
25. Ohlan A.(2016d), “Similarity Measures on Intuitionistic Fuzzy Sets,” International Journal of Science Technology and Management, 5(12), 463-468.
26. Bouchon-Meunier B., Rifqi M. and Bothorel S.(1996), “Towards general measures of comparison of objects”, Fuzzy Sets and Systems, 84, 143-153.
27. Shang X. and Jiang G.(1997), “A note on fuzzy information measures,” Pattern Recognition Letters, 18(5), 425-432.
28. Lin J.(1991), “Divergence measure based on Shannon entropy,” IEEE Transactions on Information Theory, 37(1), 145-151.
29. Fan J. and Xie W.(1999), “Distance measures and induced fuzzy entropy”, Fuzzy Sets and Systems, 104(2), 305-314.
30. Pal N.R. and Pal S.K.(1989), “Object background segmentation using new definition of entropy”, IEE Proceedings - Computers and Digital Techniques, 136(4), 248-295.
31. Couso I., Janis V. and Montes S.(2000), “Fuzzy divergence measures”, Acta Univ M Belii, 8, 21-26.
32. Montes S., Couso I., Gil P. and Bertoluzza C.(2002), “Divergence measure between fuzzy sets”, International Journal of Approximate Reasoning, 30, 91-105.
33. Hooda D.S.(2004), “On generalized measures of fuzzy entropy”, Mathematica Slovaca, 54, 315-325.
34. Havrada J.H. and Charvat F.(1967), “Quantification methods of classification processes: concept of structural α-entropy”, Kybernetika, 3(1), 30-35.
35. Parkash O., Sharma P.K. and Kumar S.(2006), “Two new measures of fuzzy divergence and their properties”, SQU Journal for Science, 11, 69-77.
36. Ferreri C.(1980), “Hyperentropy and related heterogeneity divergence and information measures”, Statistica, 40(2), 155-168.
37. Renyi A.(1961), “On measures of entropy and information”, In Proceeding of Fourth Berkeley Symposium on Mathematics, Statistics and Probability, 1, 547-561.
38. Bajaj R.K. and Hooda D.S.(2010), “On some new generalized measures of fuzzy information”, World Academy of Science, Engineering and Technology, 62, 747-753.
39. Singh R.P. and Tomar V.P.(2006), “Fuzzy information measures through generating functions”, Proceedings of Information Processing and Management of Uncertainty in Knowledge based System (IPMU), Paris, 21-28.
40. Singh R.P. and Tomar V.P.(2008), “On fuzzy divergence measures and their inequalities”, Proceedings of 10th National Conference of ISITA, 41-43.
41. Singh R.P. and Tomar V.P.(2012), “Generalized symmetric fuzzy divergence measures and their inequalities”, Presented in International Conference on History and Development of Mathematical Sciences and Symposium on Nonlinear Analysis(ICHDMS), Maharshi Dayanand University Rohtak, Haryana.
42. Singh R.P. and Tomar V.P.(2014), “On fuzzy mean divergence measures and their inequalities”, 5th National Conference at MIT, Academy of Engineering, Alandi(D), Pune, Maharashtra.
43. Singh R.P. and Tomar V.P.(2009), “Refinement of inequalities among fuzzy Means difference”, Advances in Fuzzy Mathematics, 4(2), 113-127.
44. Singh R.P. and Tomar V.P.(2010), “Refinement of inequalities among fuzzy divergence measures”, Advances in Applied Research, 2(2), 142-156.
45. Bhatia P.K. and Singh S.(2012), “Three families of generalized fuzzy directed divergence”, AMO-Advanced Modeling and Optimization, 14(3), 599-614.
46. Hooda D.S. and Jain D.(2012), “The generalized fuzzy measures of directed divergence, total ambiguity and information improvement”, Investigations in Mathematical Sciences, 2, 239-260.