IJCRR

IJCRR - 3(10), October, 2011

Pages: 190-198

Print Article   Download XML  Download PDF

DISSOCIATION ENERGIES, FRANCK-CONDON FACTORS AND R-CENTROIDS OF THE SULPHIDES OF
METALS (LI AND NI )

Author: C. Balanarayana, B.C. Venkata Reddy, R.R. Reddy, G.Venkata Chalapathi

Category: General Sciences

Abstract:The experimental potential energy curves for the different electronic states of astrophysically important
LiS+ and NiS molecules are constructed by using Rydberg-Klein-Rees method as modified by
Vanderslice et al. The ground state dissociation energies are determined by curve fitting techniques using
the five parameters Hulburt-Hirschfelder (H-H) function. The estimated dissociation energies are
0.81\?0.02 and 3.56\?0.08 eV for LiS+, and NiS respectively. These values are in good agreement with the
values reported in the earlier literature. The r-centroids and Franck-Condon factors (FC factors) for the
bands of 3 -X3 - system of LiS+ and A3 -X3 - system for NiS, molecules have been calculated. The
Franck-Condon factors are evaluated by the approximated analytical methods of Jarmain and Fraser. The
absence of the bands of these systems is explained.

Keywords: Diatomic molecules; Dissociation energies; Franck-Condon factors; r-centriods

Full Text:

I. INTRODUCTION

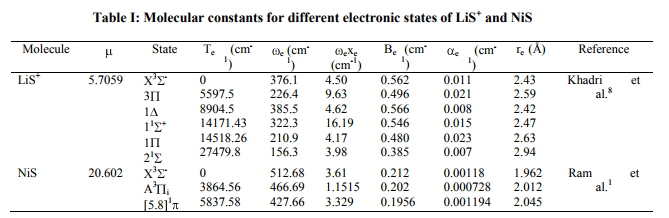
There has been considerable interest in spectroscopic studies of transition metal containing species because of their importance in chemistry, astrophysics, surface science and ab initio calculations. These compounds are widely used as catalysts in various chemical processes. Theoretical calculations on these molecules often fail to predict the correct spectroscopic properties and energy ordering of electronic states. The spectroscopic studies of these molecules, therefore, have become important to gain insight into chemical bonding in simple metal systems. Ram et al. [1] have mentioned that NiS might also be present in S-type stars. There are several theoretical studies on the spectroscopic properties of low-lying electronic states of NiS. An experimental observation of NiS has been reported by Zheng et al. [2] in the 495-555nm regions. Ram et al. [1] have reported on the observation of NiS bands in the near IR region (2500-7500 cm-1 ). Molecular species containing sulphur atom are of astrophysical importance. Some of them have been definitely identified. Theoretical investigations of the SH+ and LiS+ cations have been pursued by Khadri et al. [3]. In view of their astrophysical / scientific importance, it is proposed to construct potential curves and evaluate dissociation energies. As no attempt has been made so far to evaluate dissociation energies , Franck-Condon factors (FC factors) and r-centroids using spectroscopic data for LiS+ and NiS molecules , the present authors have taken up this investigation.

II. THEORY & COMPUTATIONAL PROCEDURE

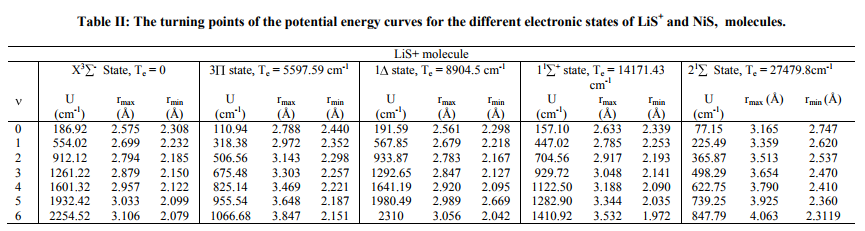
 Potential energy curves Experimental observed vibrational levels are used to construct the potential energy curve. The molecular constants required for the present study have been taken from the literature [1-4] and are listed in Table I. Many authors employed RKRV method and constructed the potential energy curves [5-16]. The RKRV [17- 21] method is an improved form of RKR method, which makes use of Wentzel-KramersBrillouin (WKB) approximation from which we obtain reliable potential energy curves with the observed vibrational and rotational constants. The potential energy curves are constructed using the method of RKRV [17-21] utilizing the molecular constants (listed in Table I) and the results are presented in Table II. The details of the said method were reported in literature, as such only the results of the present work are given Table I

Dissociation energy

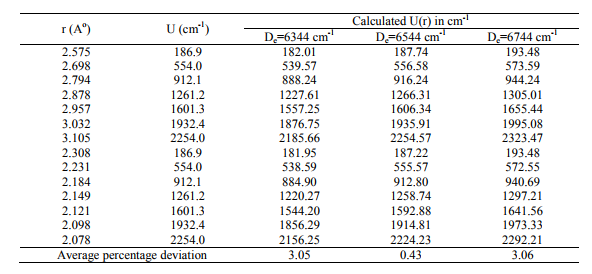
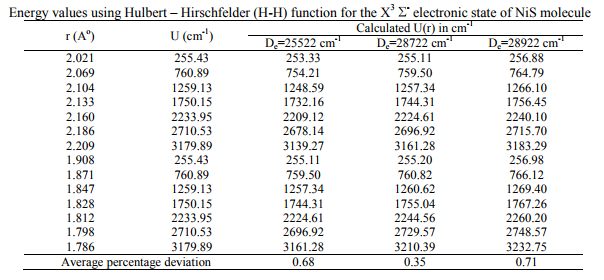
The RKRV turning points are inserted into the five parameter Hulburt-Hirschfelder‘s [22-24] function and the potential energies U(r) are calculated by varying the dissociation energy De values. An average percentage deviation is determined between the calculated U(r) and the experimental G( ) values. An accurate estimation of the dissociation energy (Do) requires an empirical potential function, which provides the best reproduction of the experimental energy values. A critical evaluation of the importance of these functions was given by Steele et al. [24] and they have shown that the potential function of HulburtHirschfelder (H-H) [22-24] fits well with the RKRV curves of a large number of diatomic molecules. In the present investigation, it is observed that the H-H function [22, 23] functions fits best and reproduces the experimental energy values (Table III). Different De values are used in the H-H function and the De value, for which the best fit of the energy values U(r) is observed, which is taken as the dissociation energy (De) of the molecule.

The values of r-Centroids of NiS molecule are estimated and presented in the Table IV. The

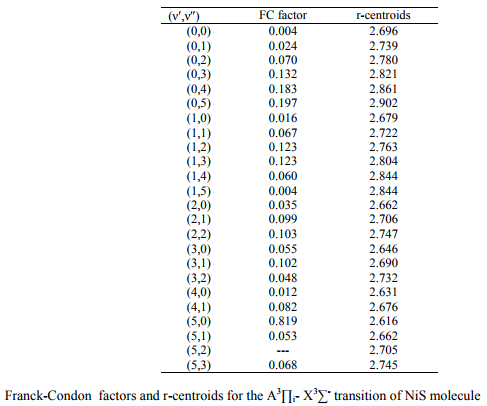
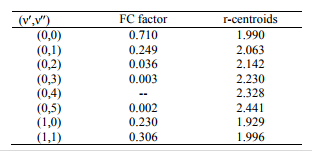
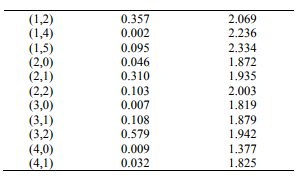
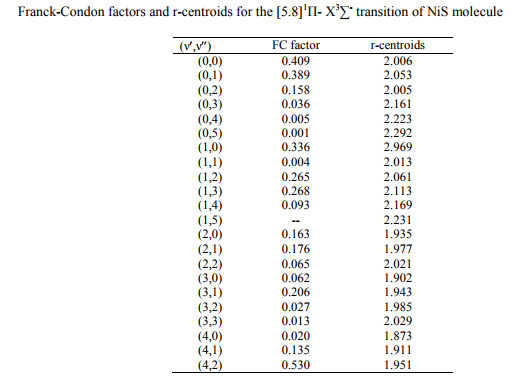
References:

1. R.S. Ram, S. Yu, I. Gordon and P.F. Bernath, J. Mol. Spectr. 20, 258 (2009).

2. X.F. Zheng, T.T. Wang, J.R. Guo, C.X. Chen andY. Chen, Chem. Phys. Lett. 137, 394 (2004).

3. F. Khadri, H.N.Dome, S.Lahman, Z. Benhakder and M. Hochalf, J. Mol. Spectr. 232, 237 (2006).

4. K.D. Setzer, F. Meinecke and E.H. Fink, J. Mol. Spectr. 56, 258 (2009).

5. R.R.Reddy and R. Viswanath, J. Astrophys. Astro. 153, 10 (1989).

6. R.R.Reddy, Y.N. Ahammed, K. RamaGopal and D. Baba Basha, J. Quant. Spectr. Radiat. Trans. 85, 105 (2004).

7. B. Narasimhamurthy and N. Rajamanickam, J. Astrophys. Astro. 53, 4 (1993).

8. R.R.Reddy and R. Viswanath, Astrophys. Space Sci., 113, 164 (1990).

9. R.R.Reddy, Y. N. Ahammed, D. Sasikala Devi, K. RamaGopal, P. Abdul Azeem and T.V.R.Rao, Astro. Phys Space Sci. 281, 729 (2002).

10. R.R.Reddy, K. Rama Gopal, Y. N.Ahammed, D. Baba Basha, K. Narasimhulu and L.S.S.Reddy, Ind. J. Pure Appl. Phys. 43, 237 (2005).

11. R.R.Reddy, Y. N. Ahammed, A.S. Rao and T.V.R. Rao, J. Quan. Spectr. Radiat. Trans. 1035, 54 (1995).

12. P. Sambasiva Rao, R. R.Reddy and D. M. Potukchi, J. Quant. Spectr. Radiat. Trans. 98, 81 (2006).

13. R. R. Reddy, Y.N. Ahammed, K. R. Gopal, P.A. Azeem and S. Anjaneyulu, Astrophys. Space Sci., 223, 262 (1999).

14. R. R. Reddy, Y.N. Ahammed, K. R. Gopal, P.A. Azeem and T.V.R.Rao, J. Quan. Spectr. Radiat. Trans. 501, 66 (2000a).

15. R. R. Reddy, Y.N. Ahammed, K. R. Gopal and D. Baba Basha, Astro. Phys. Space Sci. 286, 419 (2003).

16. J.B. Bharitya, S.H. Behere and M.L.P. Rao, J. Quan. Spectr. Radiat. Trans., 95, 43 (1990).

17. R. Z. Rydberg, Phys. 376, 73 (1931).

18. O.Z. Klein, Phys. 226, 6 (1932).

19. A.G. Rees, Proc. Phys. Soc., 938, 59 (1947).

20. J.T. Vanderslice, E.A. Masan and W.G. Lippincott, J. Mol. Spectr. 17, 3 (1959).

21. J.T. Vanderslice, E.A. Masan and W.G. Lippincott, J. Mol. Spectr. 83, 5 (1960).

22. H.M. Hulburt and J.O. Hirschfelder, J. Chem. Phys. 61, 9 (1941).

23. H.M. Hulburt and J.O. Hirschfelder, J. Chem. Phys. 1901, 35 (1961).

24. D. Steele, E.R. Linpincott and J.T. Vanderslice, Rev. Mod. Phys. 239, 34 (1962).

25. P.A. Fraser and W.R. Jarmain, Proc. Phys. Soc. 1153, 66A (1953).

26. R.W. Nicholls and W.R. Jarmain, Proc. Phys. Soc. 253, 69A (1956).

27. A.G. Gaydon, Editor, Dissociation energies and spectra of diatomic molecules, 3rd edition, Proc. Phys. Soc., 253, 69A (1968).

28. A. I.Boldrev, J. Simon and P.V. R. Senleyer, J. Chem. Phys. 99 (1993).

29. K.P. Huber and G. Hertzburg, Constants of diatomic molecules, Newyork, Nostrand, Reinhold, (1979).

30. D.R. Lide, Editor, CRC Hand Book of Chemistry and Physics, 74th edition, Tokyo, CRC press, (1993).