IJCRR

IJCRR - 4(12), June, 2012

Pages: 20-26

Date of Publication: 22-Jun-2012

EFFICIENT DISTRIBUTED ARITHMETIC BASED DISCRETE COSINE TRANSFORM CORE WITH ERROR COMPENSATION

Author: G. Dharini, Sharon P.S, Arun S, R. Radhika

Category: Technology

Abstract:In this paper, an error-compensated adder-tree is proposed to deal with the truncation errors by performing shifting and addition operations in parallel thus achieving low-error and high-throughput discrete cosine transform (DCT) design. The Discrete Cosine Transform is a type of Image Transform which expresses a sequence of finitely many data points in terms of a sum of cosine functions at different frequencies. The proposed scheme incorporates 9-bit distributed arithmetic (DA) - precision for this work instead of the 12 bits in the previous works, so as to meet the desired peak-signal-to-noise-ratio (PSNR). Thus, an area efficient DCT core is implemented to achieve 1 Gpels/s throughput rate for the PSNR requirements outlined in the earlier works.

Keywords: Distributed arithmetic (DA)-based, 2-D discrete cosine transform (DCT), PSNR – Peak Signal to Noise Ratio.

Full Text:

INTRODUCTION
Digital images have become attractive from the point of storage and transmission. Satellite and Medical images are good examples. They produce an enormous amount of digital data. Image compression is a technique of mapping images from a higher dimensional space to a lower dimensional space. The basic goal of image compression techniques is to represent an image with minimum number of bits of an acceptable image quality. There are several image compression techniques available. These techniques are generally categorized into two namely lossless and lossy techniques. The Discrete Cosine Transform has shown to be near optimal for a large class of images in energy concentration. The basis of DCT is decomposing the images into several segments or blocks and obtaining the corresponding frequency components of pixels. During the Quantization process the pixels of frequencies with less importance are discarded, hence the term lossy compression. The important frequency components are retained and they are used to reconstruct the image through the decompression process using the Inverse Discrete Cosine Transform. The loss of information during the reconstruction of the images can be controlled in this process during the compression stage. The proposed architecture operates shifting and addition in parallel by unrolling all the words required to be computed. Furthermore, the errorcompensated circuit alleviates the truncation error for high accuracy design. Based on low error Adder Tree, the DA-precision in this work is chosen to be 9 bits instead of the traditional 12 bits so as to achieve the desired peak-signal-tonoise-ratio (PSNR) requirements. Therefore, the hardware cost is very much reduced, and the speed is greatly improved using the proposed architecture.

DISCRETE COSINE TRANSFORM:
A Discrete Cosine Transform (DCT) expresses a sequence of finitely many data points in terms of a sum of cosine functions oscillating at different frequencies shown Fig 1.

All fast DCT implementations usually try to avoid multiplication operations by increasing the number of addition operations and decreasing the number of multiplication operations. Addition actually makes the architecture slow as the time complexity for addition is almost the same as that of fast multipliers.

DISTRIBUTED ARITHMETIC:
Distributed Arithmetic (DA) is an efficient method for computing inner products when one of Distributed arithmetic is an efficient method for the input vectors is fixed. Look-up tables and accumulators are used instead of multipliers for computing inner products and has been widely used in many DSP applications such as DFT, DCT and convolution. In particular, there has been great interest in implementing DCT with distributed arithmetic and in reducing the ROM size required in the implementations since the DA-based DCT

A. Derivation:
Distributed Arithmetic is proposed to realize inner product of vectors with optimal solutions in terms of hardware requirement. This features implementation without the need of multipliers, and at the same time, without the need of ROM as in DA approach.

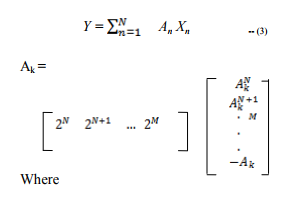
A is a set of predetermined coefficients, and x are data values. Assume that the coefficient an is Q-bit two‘s complement binary fraction number. The above equation can be expressed as follows:

Thus, the inner product computation can be implemented by using shifting and adders instead of multipliers. Therefore, low hardware cost can be achieved by using DA architecture.

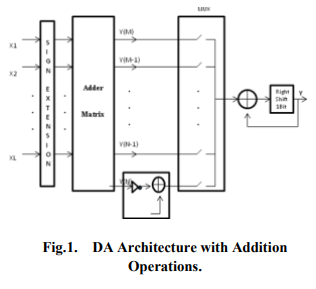
In this figure, input signals are sign extended bits and then fed into the Adder Matrix, which is a butterfly structure with number of output lines determined by DA precision.

B. Error Compensation:
NEDA architecture is the smallest architecture for DA-based DCT designs, but speed limitations exist in the operations of serial shifting and addition after the DA-computation.

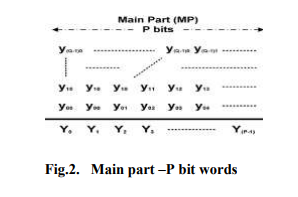
The high-throughput shift-adder-tree and addertree, those unroll the number of shifting and addition. However, a large truncation error occurred. In order to reduce the truncation error, several error compensation methods have been presented based on statistical analysis of the relationship between partial products and multiplier-multiplicand. However, the elements of the truncation part are independent so that the previously described methods cannot be applied.

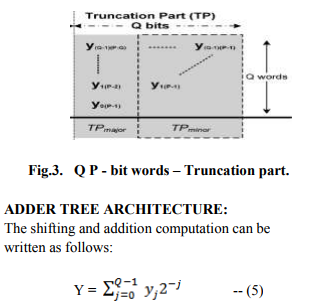
The shifting and addition computation uses a shift-and-add operator in VLSI implementation in order to reduce hardware cost. However, when the number of the shifting and addition increases, the computation time will also increase. Therefore, the shift-adder-tree presented in operates shifting and addition in parallel by unrolling all the words needed to be computed for high-speed applications. However, a large truncation error occurs and an ECAT architecture is proposed to compensate for the truncation error in high-speed applications. The shifting and addition output can be expressed as follows:

Considering high-speed implementation, the proposed 2-D DCT is designed using two 1-D DCT cores and one transpose buffer. The DAprecision and transpose buffer word lengths are chosen to be 9 bits and 12 bits, respectively, so that the system can meet the PSNR requirements stated in previous works. The proposed 8 x 8 2-D DCT core has a latency of 10 clock cycles and is operated at 125 MHz. As a result of the 8 parallel outputs, the core can achieve a throughput rate of 1 Gpixels per second.

ECAT with Other Architectures Fig. 7 shows a DA-Butterfly-Matrix, that includes two DA even processing elements (DAEs), a DA odd processing element (DAO) and 12 adders/subtractors, and 8 ECATs. The eight separated ECATs work simultaneously, enabling high-speed applications to be achieved. After the data output from the DA-ButterflyMatrix is completed, the transform output will be completed during one clock cycle by the proposed ECATs.

RESULT AND CONCLUSION The tables 1 and 2 show the performance characteristics of the proposed design and the comparison of the proposed with the older architectures. Thus a high-speed and low-error 8 x 8 2-D DCT design with ECAT is proposed to improve the throughput rate significantly at high compression rates by operating the shifting and addition in parallel. The proposed errorcompensation minimizes the truncation error in ECAT. Fig.8 shows the VHDL simulation result obtained using Xilinx ISE Simulator for proposed 1D DCT architecture. The DAprecision can be chosen as 9 bits instead of 12 bits so as to meet the PSNR needs. Thus, the proposed DCT core has the highest hardware efficiency than those in previous works. Finally, an area - efficient 2-D DCT architecture is implemented with a maximum throughput rate of 1 Gpixels/s.

ACKNOWLEDGEMENT Authors acknowledge the immense help received from the scholars whose articles are cited and included in references of this manuscript. The authors are also grateful to authors / editors / publishers of all those articles, journals and books from where the literature for this article has been reviewed and discussed

References:

1. Y.Wang, J. Ostermann, and Y. Zhang, Video Processing and Communications, 1st ed. Englewood Cliffs, NJ: Prentice-Hall, 2002.

2. Y. Chang and C.Wang, ?New systolic array implementation of the 2-D discrete cosine transform and its inverse,? IEEE Trans. Circuits Syst. Video Technol., vol. 5, no. 2, pp. 150–157, Apr. 1995.

3. White, S.A, .Applications of distributed arithmetic to digital signal processing: a tutorial review., ASSP Magazine, IEEE, Volume: 6 Issue: 3 , Jul 1989, Page(s): 4 - 19

4. S. Uramoto, Y. Inoue, A. Takabatake, J. Takeda, Y. Yamashita, H. Yerane, and M. Yoshimoto, ?A 100-MHz 2-D discrete cosine transform core processor,? IEEE J. Solid-State Circuits, vol. 27, no. 4, pp. 492–499, Apr. 1992.

5. S. Yu and E. E. S. , Jr., ?DCT implementation with distributed arithmetic,? IEEE Trans. Comput., vol. 50, no. 9, pp. 985–991, Sep. 2001.

6. A. Shams, A. Chidanandan, W. Pan, and M. Bayoumi, ?NEDA: A low power high throughput DCT architecture,? IEEE Transactions on Signal Processing, vol.54(3), Mar. 2006.

7. Peng Chungan, Cao Xixin, Yu Dunshan, Zhang Xing, ?A 250MHz optimized distributed architecture of 2D 8x8 DCT,? 7th International Conference on ASIC, pp. 189 – 192, Oct. 2007.

8. M. Kovac, N. Ranganathan, ?JAGUAR: A Fully Pipelined VLSI Architecture for JPEG Image Compression Standard,? Proceedings of the IEEE, vol.83, no.2, pp. 247-258,Feb.1995.

9. Yi Yang; Chunyan Wang; Omair Ahmad, M.; Swamy, M.N.S., .An on-line CORDIC based 2-D IDCT implementation using distributed arithmetic., Sixth International Symposium on Signal Processing and its Applications,. 2001 , Vol. 1

10. Wilton, S.J.E.; .Embedded memory in FPGAs: recent research results., Communications, Computers and Signal Processing, 1999 IEEE Pacific Rim Conference on , 1999 , Page(s): 292 -29