IJCRR

IJCRR - 5(15), August, 2013

Pages: 102-110

Date of Publication: 17-Aug-2013

THERMOSOLUTAL INSTABILITY OF AN INCOMPRESSIBLE, VISCOUS FLUID CONFINED IN A POROUS MEDIUM IN THE PRESENCE OF MAGNETIC FIELD

Author: Arti Bansal

Category: Technology

Abstract:The paper critically examines, within the framework of linear analysis, thermosolutal instability of an incompressible, viscous fluid confined in a porous medium in the presence of magnetic field, analytically and numerically both. The analytical discussion provides the sufficient conditions of stability and instability and the characterization of modes. By actually calculating the root of eigenvalue equation (of degree 4) neutral stability curves are drawn. The numerical results show the effect of various physical parameters on the critical wave number ac. It is concluded that RD-1 , S and R4 have stabilizing character and Richardson number J has destabilizing character. The non-dimensional parameter R2 shows a dual character, which depends upon thermal diffusivity ?

Keywords: Thermosolutal instability, porous medium, magnetic field

Full Text:

INTRODUCTION
The problems on thermal instability (Bénard convection) in a fluid layer under varying assumptions of hydrodynamics and hydromagnetic have been discussed in detail by Chandrasekhar[1] in his celebrated monograph. The problem of thermosolutal instability in fluids through a porous medium is of importance in geophysics, soil sciences, ground-water hydrology and astrophysics. The development of geothermal power resources holds increased general interest in the study of the properties of convection in a porous medium.The instability of fluid flows in a porous medium under varying assumptions has been well summarized by Scheidegger [2] and Yih [3]. While investigating the flows or flow instabilities through porous media, the liquid flow has been assumed to be governed by Darcy’s Law [4] by most of the research workers, which neglects the inertial forces on the flow. Beavers et al. [5] demonstrated experimentally the existence of shear within the porous medium near surface, where the porous medium is exposed to a freely flowing fluid, thus forming a zone of shearinduced flow field. Darcy’s equation however, cannot predict the existence of such a boundary zone, since no macroscopic shear term is included in this equation (Joseph and Tao [6]). To be mathematically compatible with the Navier-Stokes equations and physically consistent with the experimentally observed boundary shear zone mentioned above, Brinkman [7] proposed the introduction of the term 1 k μ V in addition to μ 2  V in the equations of fluid motion. The thermosolutal convection in a porous medium was studied by Nield and Bejan [8]. Instability of compressible or incompressible flow has been studied extensively by a number of research workers in past few decades. In almost all such investigations, the Boussines’q approximation is used to simplify the equations of motion. Goel et.al. [9] examined the shear flow instability of an incompressible viscoelastic second order fluid in a porous medium in which the modified Darcy’s law is replaced by the celebrated Brinkman model so that both the inertia and viscous terms are included in their usual forms. The behaviour of conducting fluid is very much different in the absence and in the presence of a magnetic field. The interesting properties associated with a magnetic field, have attracted a number of research workers to work in this direction. Bansal and Agrawal [10] have studied the thermal instability of a compressible shear flow in the presence of a weak applied magnetic field. The problem for compressible shear layer in the presence of a weak applied magnetic field through porous medium has been studied by Bansal et.al. [11]. In the present paper, an attempt has been made to examine the thermosolutal instability of an incompressible, viscous fluid in the presence of magnetic field and confined in a porous medium following Brinkman model. The Boussinesq approximation is used throughout the paper. It states that variations of density in the equations of motion can safely be ignored everywhere except its association with the external force. The approximation is well justified in the case of incompressible fluids.

FORMULATION OF THE PROBLEM
Here we consider an infinite, horizontal, incompressible, viscous fluid saturating an isotropic porous medium and which is subjected to uniform magnetic field in the horizontal direction. Uniform temperature and concentration gradients are maintained along z-axis. Equations expressing the conservation of momentum, mass, magnetic field, temperature, solute mass concentration and equation of

NUMERICAL RESULTS AND DISCUSSION
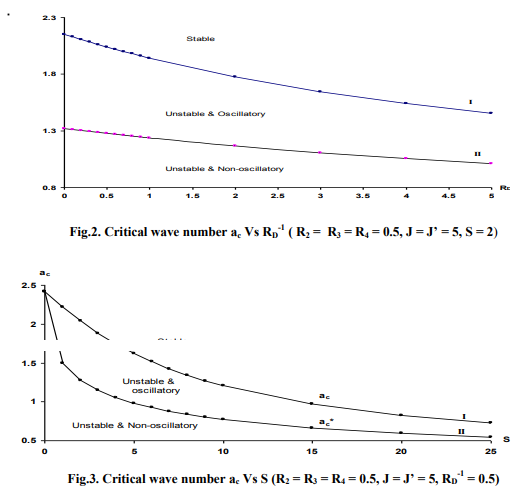
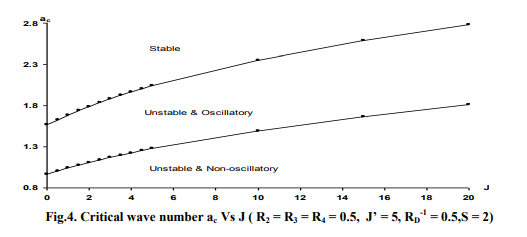
Eq.(10) is a fourth degree equation in ? with real coefficients, which depends upon RD -1 , S, J, J’, R2, R3, R4, l and a. Our aim has been to examine the effect of various parameters such as RD -1 , R2, R4, magnetic force number S and the Richardson number J on the stability of the system. This has been achieved by actually calculating the roots of the equation (3.2) correct upto three decimal places. The calculation of critical wave numbers has lead to the neutral stability curves. Fig.2. shows the critical wave number ac for different value of RD -1 (curve-I). When RD -1 =0, for a < 1.321 unstable modes are non-oscillatory i.e., the eigenvalue equation has all real roots with at least one positive root. For 1.321 < a < 2.153 unstable modes are oscillatory and system becomes stable for a ≥ 2.153 . As RD -1 increases, ac decreases so that the range of stable wave numbers increases. It is concluded that RD -1 has a stabilizing character and a large value of RD -1 is required to stabilize the system for all wave numbers. Curve-II separates the unstable modes into unstable oscillatory and unstable nonoscillatory modes. As RD -1 increases, the range of both the unstable oscillatory and the unstable nonoscillatory modes decreases. Fig.3. shows the stabilizing character of magnetic field (curve-I). Short wave length perturbations are more stable. The unstable modes are divided into oscillatory and non-oscillatory modes. The large wave length perturbations are unstable and nonoscillatory and the modes which are intermediatory between stable and unstable nonoscillatory modes are unstable and oscillatory, i.e., a > ac are stable, ac* < a < ac are unstable and oscillatory and a < ac* are unstable and nonoscillatory. It is important to observe that whereas the unstable modes are non-oscillatory in the absence of magnetic field, some oscillatory unstable modes are introduced in its presence . Fig.4. shows the destabilizing character of J. As J increases, ac increases which decreases the range of stable wave numbers. As is clear from this figure, the range of both the non-oscillatory unstable and the oscillatory unstable modes increases with J. Fig.5. shows the dual character of the nondimensional parameter R2, which in fact, depends upon the thermal diffusivity ?. As R2 increases from 0 to 0.3, the range of stable wave increases. As R2 increases from 0.3 to 3.5 approximately, the range of unstable wave numbers decreases rapidly, however, this decrease in the range of unstable wave numbers is slow as R2 further increases beyond 3.5. The neutral stability curve also shows that the critical wave number for maximum instability is given by ac = 2.081 and it occurs for R2 = 0.3. Similar character is exhibited for R3. Stabilizing character of fluid viscosity is exhibited in Fig.6. As R4 increases, the range of stable wave numbers increases sharply upto R4 = 4 (approx.) and then increases slowly as R4 further increases.

CONCLUSION
The analytical discussion provides the sufficient conditions of stability and instability and the characterization of modes. Theorem 2 states that non-oscillatory modes are stable if ? ? 0 and 0 ' ? ? . This situation is known as potentially stable arrangement. The numerical results show the effect of various physical parameters on the critical wave number ac . On the basis of numerical discussion & neutral stability curves obtained in paper, it is concluded that medium porosity parameter RD -1 , magnetic force number S and fluid viscosity have stabilizing character and Richardson number J has destabilizing character. The non-dimensional parameter R2, which depends upon thermal diffusivity ?, shows a dual character,

ACKNOWLEDGEMENT
The author is grateful to Professor S.C. Agrawal, Retd. H.O.D., Department of Mathematics, C.C.S. University, Meerut, for providing valuable support.

References:

1. Chandrasekhar S., Hydrodynamic and Hydromagnetic Stability. – Oxford, UK: Clarendon Press, 1961.

2. Scheidegger A. E. Growth of instabilities on displacement fronts in porous media. Phys Fluids 1960; 3 94.

3. Yih C. S. Flow of a non-homogeneous fluid in a porous medium. J. Fluid Mech. 1961; 10 133.

4. H. Darcy Les fontaines publiques de la ville de Dijon Paris : Victor Dalmont (1856).

5. Beavers G.S., Sparrow E.M. and Magnuson R.A. , Experiments on coupled parallel flows in a channels and a bounding porous medium. – J. Basic Engng. Trans. 1970, ASME, vol.D92, pp.843-845.

6. Joseph D.D. and Tao L.N., The effect of permeability on the slow motion of a porous sphere in a viscous liquid, 1964.

7. Brinkman H. C. A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles 1947; Appl. Sci. Res., A1 27.

8. Nield D. A. and Bejan A. Convection in porous medium 1992; Springer.

9. Goel A. K., Agrawal S. C. and Jaimala shear flow instability of an incompressible viscoelastic second order fluid in a porous medium. Indian J. pure appl. Math. 1997 28(4) 563.

10. Bansal N. and Agrawal S. C. thermal instability of a compressible shear flow in the presence of a weak applied magnetic field. Proc. Nat. Acad. Sci. India 1999 ;69(A) III .

11. Bansal A., Bansal N. and Agrawal S. C. Thermal instability of compressible shear layer in a porous medium in the presence of a weak applied magnetic field. Ganita 2004; vol.55, no.2,187-197.

12. Goel A. K., Agrawal S. C. and Agarawal G.S. Hydromagnetic stability of an unbounded couple stress binary fluid mixture having vertical temperature and concentration gradients with rotation.Indian J. pure appl. Math. 1997; 30(10) 991.