IJCRR

IJCRR - 5(1), January, 2013

Pages: 13-31

Print Article   Download XML  Download PDF

CORRELATION OF ELECTRON SPIN RESONANCE, NUCLEAR QUADRUPOLE RESONANCE, REFLECTANCE AND MAGNETIC PARAMETERS OF Ti (II, III), V (II, III &IV) AND Cr (III) COMPLEXES: A DFT STUDY

Author: Harminder Singh, A. K. Bhardwaj, M. L. Sehgal, Susheel K. Mittal

Category: General Sciences

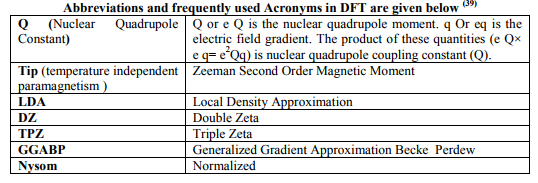
Abstract:DFT implemented by ADF2010.02 was applied to calculate and correlate 14 ESR, NQR, reflectance and magnetic parameters of the first transition metal ion complexes. Commands like Single Point, LDA, Default, Spin Orbit, Unrestricted, None and Collinear were applied to the software using DZ or TPZ Basis sets.36 complexes such as [TiX4]- (X=F, Cl, Br, I), [TiX4]2- (X=F, Cl, I), [TiX6]3-,4- (X=F, Cl, Br I),[Ti(OH2)4]2+,3+, [VF4]0,1- (X=F, Cl, Br I), [VX6]4- (X = F, Cl, Br I), [V(H2O)6]+2, [CrX6]3- (X= F, Cl, Br, I, CN) and [Cr (NH3)]3+ having both the regular (Td, Oh) and the distorted stereochemistries (C1, D4h , D6h , D12 and S4) were selected to carry out all the computations in the gas phase. In [TiX6]4- (X= Br, I), LDA was replaced by GGABP. Spin Polarization was kept equal to the number of unpaired electrons present in the metal ions respectively. All the complexes possessed a Nysom symmetry and definite Pre-optimization .The software gave ESR (g11, g22, g33, giso, a11, a22, a33, Aten ), NQR [?, q11, q22, q33, NQCC] and optimization parameters [bonding energy, total energy having contributions from LDA and GGA components]. Two more ESR parameters [H^, ΔEhf] were calculated from these parameters. Also, two Reflectance parameters [? complex, % covalent character] were obtained from the giso parameter. Again, five magnetic parameters [?soc, ?t, ?net, t2g electron delocalization and its constant k] were derived from ESR and Reflectance parameters. Lastly, the Laplace equation was verified from the NQR parameters (q11, q22, q33,).The values of the ESR parameter like t2g electron delocalization constant (k) agreed well with the Reflectance parameter namely Nephelauxetic ratio (?35) because both determine the % covalent character in the complexes. The values of all the parameters calculated by the selective use of 18 relations would change with the change in oxidation states of the metal ions but were always in agreement with their reported values.

Keywords: DFT, Nephelauxetic ratio, Pre-optimization.

Full Text:

INTRODUCTION

Effective Spin Hamiltonian (H^) is a mathematical expression that determines the energy of an ESR transition in a paramagnetic complex. It depends upon the ESR [anisotropic and isotropic splitting factors (g11, g 22, g 33, g iso), hyperfine coupling constants (a11,a22, a33, A ten)] and NQR [electric field gradient or efg (q11,q22, q33), Nuclear Quadrupole Constant (Q)]* parameters, (S), (?e), (?n), (I), ( g n) and nature of the surrounding nuclei possessing quadrupole moments (I?1).

The following points necessitated the present study to be taken up with the help of software: There had hardly been any attempt made to theoretically calculate and correlate ESR, NQR, Reflectance and Magnetic parameters of transition metal ion complexes.

I. Theoretical calculation of (H^) of the complexes was never reported before as a class. II. With ESR transitions falling in low energy microwave region (X band: 9000-10000 MHz), the experiments required cumbersome cryoscopy conditions.

With certain commands, the ADF 2010.02 software gave the five ESR and NQR parameters. They were together used to calculate two other ESR parameters [effective spin Hamiltonian (H^) and hyperfine coupling energy (?E hf).The giso parameter was further correlated to two Reflectance parameters [spin orbit coupling constant (?complex), % covalent character]. Again, ESR and Reflectance parameters were together used to calculate and correlate five magnetic parameters [magnetic moments like total (?t), net (?net) and that containing contributions from spin and orbital (?soc or ?ADF), t2g electron delocalization and its constant (k)].

This communication is an extension of our previous work (1). Here, we have calculated and correlated parameters of 36 Ti(II,III),V(II,III,IV) and Cr(III) complexes such as [TiX4] 1- (X=F, Cl, Br, I), [TiX4] 2- (X=F, Cl, I), [TiX6] 3-,4- (X=F, Cl, Br I), [Ti(OH2)4] 2+,3+, [VF4] 0, 1- (X=F, Cl, Br I), [VX6] 4- (X=F, Cl, Br I), [V(H2O)6] 2+ ,[CrX6] 3- (X= F, Cl, Br, I, CN) and [Cr(NH3)]3+ having both regular (Td ,Oh) and distorted stereochemistries (C1,D4h, D6h , D12 , S4).We applied DFT(2-3) implemented in ADF 2010.02 software to obtain 5 parameters (g, a, q, NQCC, ?) which were further used to calculate 9 more parameters [H^,?E hf, ? complex, % covalent character, ?t , ?net, ?soc, t2g electron delocalization and its constant (k)].

(1) Calculation of ESR Parameters(4-12) Effective Spin Hamiltonian (H^) and Hyperfine Coupling Energy (?E h f)

Four contributing factors to H^ are: g, a, Q and interaction of nuclear magnetic moment with external magnetic field (I).Relations [1-3] having contributions from these four factors were used to calculate H^. The Hyperfine Coupling Energy (?E h f) was calculated by relations [4]. Relation [1] was used for systems with different values of g and a. [2] Was applied to axially symmetric systems. [3] Was applied if the systems had the same values of both a and g or g only. The first and the last terms in these relations were in ergs and the other two were in MHz (6.627 ? 10-21 erg = one MHz; ?e=1.3994 MHz/Gauss; ?n =?e /1836. g n has a specific value for each metal). ?Eh f and Q are in MHz).

(2) Calculation of NQR parameters (13-14) Asymmetry Coefficient (?) and Laplace Equation are calculated by relations [5-6]. Relations [1-6] are given under Table: 1. 5 A.

Relations used for calculating Reflectance and Magnetic parameters (15-20)

Parameters like ?soc, ?t , ?net, t2g electron delocalization (all in B.M), its constant k and ?complex (both in cm-1 ) were calculated by relations [7-18] given below the Table: 1. 6 B. ? soc was the magnetic moment from the spin orbit coupling and (?t) represented the total magnetic moment. ?tip and ?tip were the Zeeman Second Order molar magnetic susceptibility and Zeeman Second Order magnetic moment. ?Mol .s. o , always represents the molar magnetic susceptibility from ? s. o (1250.0Χ10-6 , 3333.3Χ10-6 and 6250.0Χ10- 6 c g s /mol with 1, 2 and 3 unpaired electrons respectively).?t was the total molar magnetic susceptibility and k was t2g electron delocalization constant. n =8 or 4 for A or E ground terms respectively. ?Metal ion and ?complex were the spin-orbit coupling constant of metal ions in different oxidation states when free and when they form complexes [?Ti (II,III) = 61.5, 155.0 ; ?V(II,III,IV) = 56.7, 105.0, 250.0 and ?Cr(III) = 92.0 ]. ?complex and ?Metal ion possessed different values. The g t and g eff were the total and effective values of g respectively. The former made use of the results obtained from the software while the latter used the reflectance parameters from the literature. The constant A=1.5 for Ti (II, III) in the relation [18].

METHODOLOGY

After optimization of the complexes on ADF 2010.02, the software was run with Single Point, LDA*, Default, Spin Orbit, Unrestricted, None and Collinear commands by using DZ* or TPZ* Basis sets for all the Ti (II, III), V (II, III, IV) and Cr (III) complexes except [TiX6] 4- (X= Br, I) where LDA was replaced by GGABP*. All the complexes had Nysom* symmetry.

[I]- Complexes of Ti (II andIII) Ti (II) is a non –Kramer ion. The degeneracy of its m j states is always completely removed even by the crystal field to give only singlet m j levels. [a] (i) With no spin –orbit coupling in tetrahedral Ti (II) complexes having 3A2 ground term, we would expect longer relaxation times to observe their ESR spectra easily. Of course, the electron cloud of 3A2 ground term of Ti (II) would intermix with its higher 3 T2 term of the same multiplicity to make 3A2 to acquire some T character. A weak spin –orbit coupling would operate but with hardly any affect on the relaxation times.

(ii) Only a few examples of ESR spectra of octahedral complexes of Ti (II) having 3T1g ground state were reported due to the presence of extensive spin -orbit coupling.

b] (i) Although, tetrahedral Ti (III) complexes with 2E ground term did not possess any spinorbit coupling, yet the electron cloud of the 2E term would intermix with electron cloud of its higher 2T2 term to make 2E term to acquire some T character. A weak spin –orbit coupling would operate but without affecting the relaxation times. So their ESR spectra were easy to observe.

(ii)Ti (III) octahedral complexes (21) with ground term 2 T2 g, always experience a considerable spin orbit coupling which shortens their spin relaxation times.ESR experiments in such cases were observed only at the liquid helium temperatures.

No doubt, some work had been reported on Reflectance and Magnetic data of Ti (II, III) complexes (22-23) , yet more study is needed to correlate their ESR, NQR, Reflectance and Magnetic parameters.

RESULTS

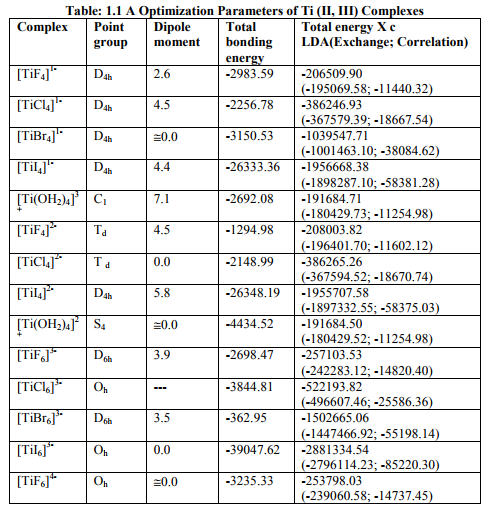
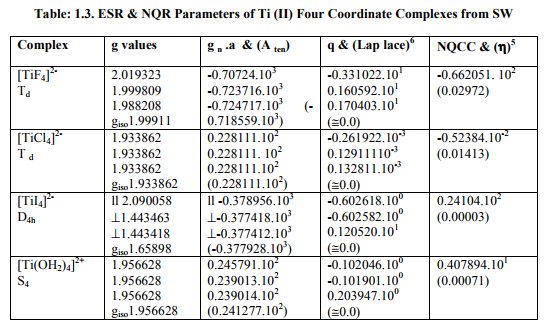
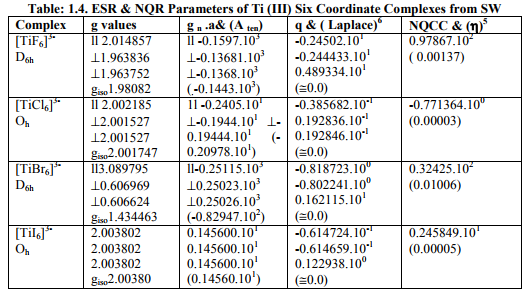
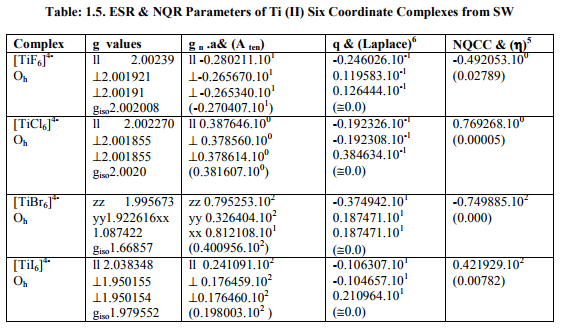
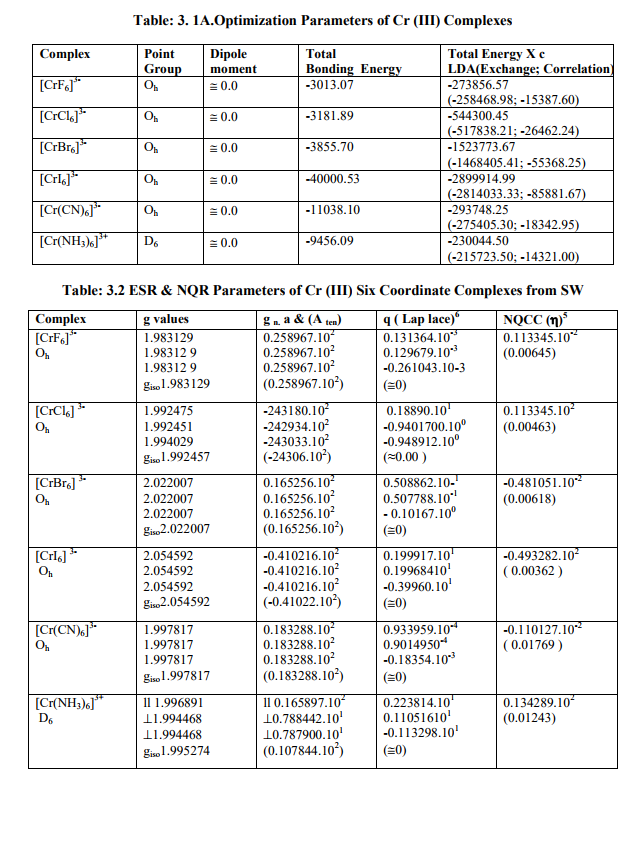
Each Output file of a complex gave values of two ESR (g11, g22 , g33 and g iso, product of g n and a11,a22,a33,Aten) and three NQR(?,q11,q22,q33, NQCC) parameters along with its optimization parameters[point group, dipole moment, bonding energy and total energy (X c)]. X c was made up of LDA and GGA components, each one further contained Exchange and Correlation parts]. The bonding energy was computed as an energy difference between molecule and fragments. With the fragments being single atoms, they were usually computed as Spherically Symmetric and Spin-Restricted. So this might not represent the true atomic ground state (24-25).

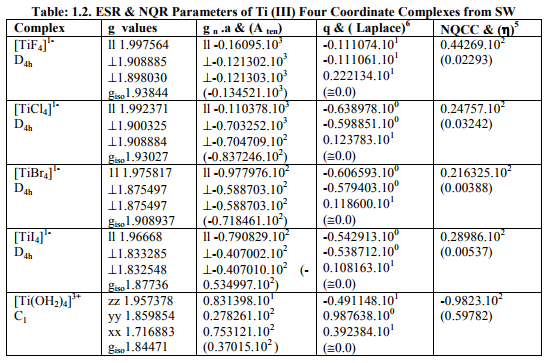
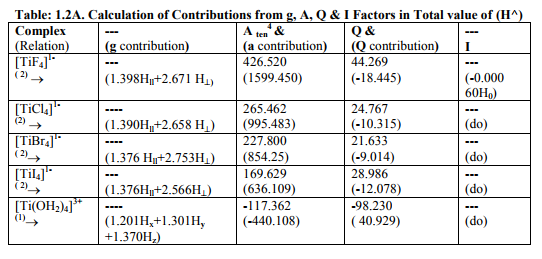
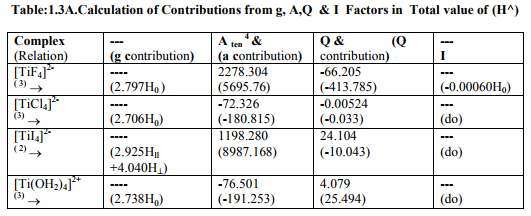
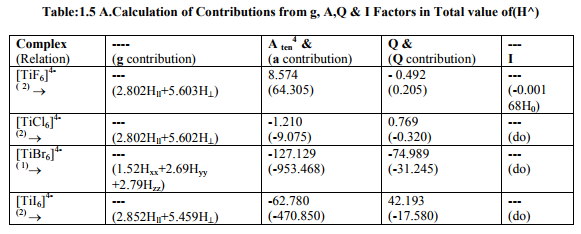
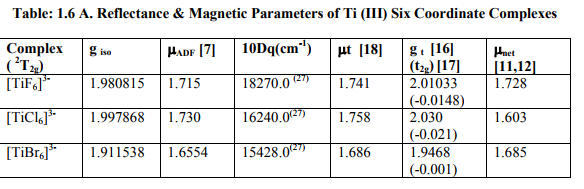
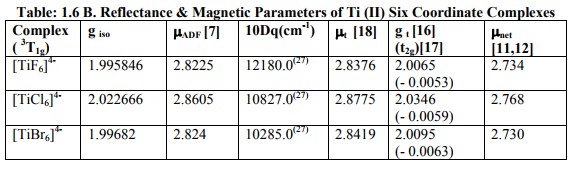
Tables: 1.1 and 1.1A contained values of the optimization parameters of the Ti (II, III) complexes. Tables: 1.2 -1.5 gave values of all the five ESR and NQR parameters and verification of Laplace equation for four and six coordinate Ti (II, III) complexes respectively. Table: 1.2A -1.5 A gave giso, Aten and Q values along with contributions from their respective factors and also contribution from the fourth factor called interaction of nuclear magnetic moment with external magnetic field factor (I) into H^. They also contained their ?Eh f (≈ 0.5 A ten) values. The magnetic parameters of 10 out of the 17 complexes were given in Tables: 1.6, 1.6 A and 1.6 B.

DISCUSSION

The discussion regarding Ti (II, III) complexes was divided into two parts:

[A] Calculation of ESR and NQR parameters: (a) Effective Spin Hamiltonian (H^):

Depending upon the symmetries and the values of parameters, the complexes were categorized as:

i) [Ti X4] 1- (X=F, Cl, Br, I) possessed characteristics of D4h axial symmetry with (a) Two of three g called g? were of same value and third of higher value called g?? . (b) Two of three a called a? parameters were of same value and third of higher value called a11. (c) Two of the three q parameters had same value. (d) ?=0. Relation [2] was applied to calculate their H^.

ii) [Ti (OH2)4] 3+ possessed C1 symmetry and different g and a values. Relation [1] was applied to calculate its H^.

iii) [Ti I4] 2- had characteristics of axial symmetry. Relation [2] was used to calculate its H^.

iv) [TiX4] 2- (X=F, Cl) and [Ti (OH2)4] 2+ were of Td and S4 symmetries respectively with same g and a values. Relation [3] was applied to calculate their H^.

v) [TiX6] 3- (X= F, Cl, Br) possessed D6h, Oh, D6h symmetriesrespectively but showed characteristics of D4h axial symmetry. Relation [2] was applied to calculate their H^.

vi) [TiI6] 3- possessed Oh symmetry with same g and a values. So its H^ was calculated by [3].

vii) [TiX6] 4- (X= F, Cl, I) possessed Oh symmetry but showed characteristics of D4h axial symmetry. Relation [2] was applied to calculate their H^.

viii) [TiBr6] 4- had distorted Oh symmetry with different values of g and a. Relation [1] was applied to calculate its H^. (Put S_x=S_y=S_z=1/2 for Ti3+ and 1 for Ti2+; I_x=I_y=I_z=2.5 and g n = - 0.315392). Values written in small brackets in horizontal rows at end of each complex (Tables: 1.2A-1.5A) gave contributions from four factors (?), i.e. g, a, Q and (I) into H^

(b) Verification of Laplace equation and parameters such as ? (Tables: 1.2-1.5) and ?E hf (Tables: 1.2 A-1.5 A) were calculated by relations 6, 5 and 4 respectively.

[B] Calculation of Reflectance and Magnetic parameters from ESR parameters:

It included calculation of ?ADF, ?tip, ?tip, ?t , ?net, gt , t2g electron delocalization,its constant (k), ?complex and % covalent character(26) . It may be noted that:

(i) No authentic 10 D q data of [TiI4] 1- , [TiI4] 2- , - 3- , [TiI6] 2- , 3- , [TiX4] 2- (X=F, Cl) were found in literature. So calculations of magnetic parameters of these 7 complexes were omitted.

(ii) [Ti X6] 3- (X= F, Cl, Br) with one unpaired electron possessed small magnetic moments and negligible t2g electron delocalization. So, their ?complex ? free ?Ti (III) = 155.0 cm-1 .

(iii) [Ti X6] 4- (X= F, Cl, Br) also should have very small t2g electron delocalization due to small ?Ti (II) [61.2 cm-1 ].So their ?complex and % covalent character were not calculated.

(iv) ?ADF of these complexes was somewhat less than the spin only values of Ti (II, III). (a) Table: 1.6 contained [Ti X4] 1- (X=F, Cl, Br) and [Ti (H2O) 4] 3+ with 2E ground term for Ti (III). All the magnetic parameters were calculated by applying already given relations. (b) Table: 1. 6 A contained [TiX6] 3- (X= F, Cl, Br) with 2T2g ground term for Ti (III).All the parameters except t2g electron delocalization and % covalent character were calculated. (c) Table: 1.6 B contained [TiX6] 4- (X= F, Cl, Br) with 3T1g ground term Ti (II). All the parameters except t2g electron delocalization and % covalent character were calculated.

[II] Complexes of V (II, III, IV) and Cr (III)

Some work has already been reported on Reflectance and Magnetic properties (28-29) of V (II, III, IV) complexes. But, quite a large number of papers are reported on Cr3+ complexes (31-38) Still a detailed study was needed to know as to how parameters of a metal change with change in its oxidation states. V (IV), V (II) and Cr (III) are Kramer ions and V (III) is a non –Kramer ion.

(a) Both V (II) and Cr (III) [Oh] have 4A2g ground state. Therefore, they should show Zero Field Splitting (D) and Jahn -Teller effect. But in [VX6] 4- (X=F, Cl, Br, I), [V (OH2)6] 2+, [CrX6] 3- (X= F, Cl, Br, I, CN), [Cr (NH3)] 3+, the ligands were so chosen that either octahedral or nearly octahedral symmetry was enforced. So Jahn - Teller effect was neglected. The software was so designed that did not account for Zero Field Splitting.

(b) Because of the presence of extensive spin orbit coupling in 3T2g ground term, only a few examples of ESR spectra of V (III) [Oh] complexes had been reported.

In V (III) [Td] complexes with 3A2 ground term and no spin –orbit coupling, longer relaxation times were expected. Hence their ESR spectra were easy to observe. Of course, an intermixing of electron cloud of its ground 3A2 term with higher 3T2 term of the same multiplicity should cause 3A2 term to acquire some T character to allow week spin orbit coupling. But this weak coupling would hardly affect the relaxation times.

(c) In V (IV) [Oh] complexes, the ground term 2T2g should experience a considerable spin orbit coupling to make their ESR spectra difficult to observe.V (IV) [Td] complexes having 2E ground term did not possess any spin-orbit coupling.

But an intermixing of its 2E ground term with higher 2T2 would make it to acquire T character. As it did not affect relaxation times, their ESR spectra were easy to observe.

RESULTS

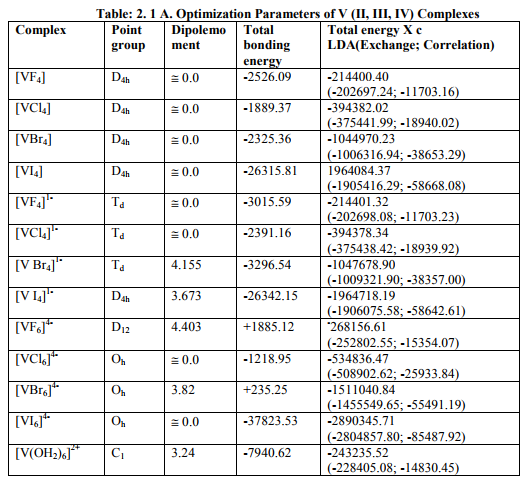
(A) Tables: 2.1, 2.1 A and 3.1, 3.1 A contained some optimization parameters of vanadium, chromium metals as well as of the V (II, III, IV) and Cr (III) complexes.

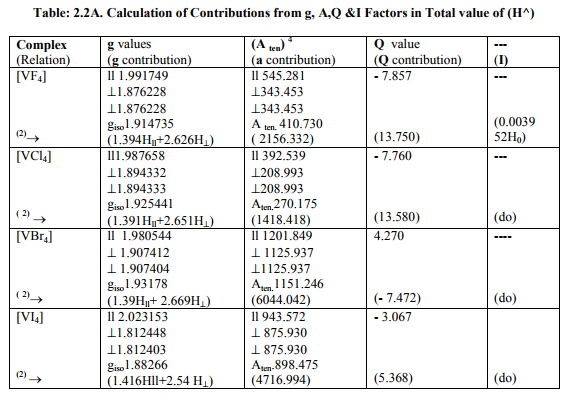
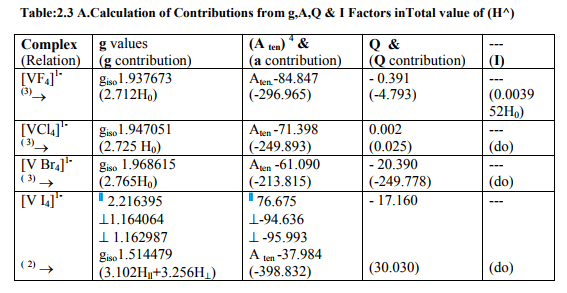
(B) Tables: 2. 2 -2.4 and 3.2 give values of all the five ESR and NQR parameters for V (II, III, IV) and Cr (III) complexes respectively.

(C) Tables: 2. 2 A -2.4A and 3.2 A give g iso, A ten and Q values and contributions from their respective factors along with contribution from the fourth factor (I) into H^ and ?Eh f (≈ 0.5 A ten) for V (II,III,IV) and Cr (III) complexes respectively

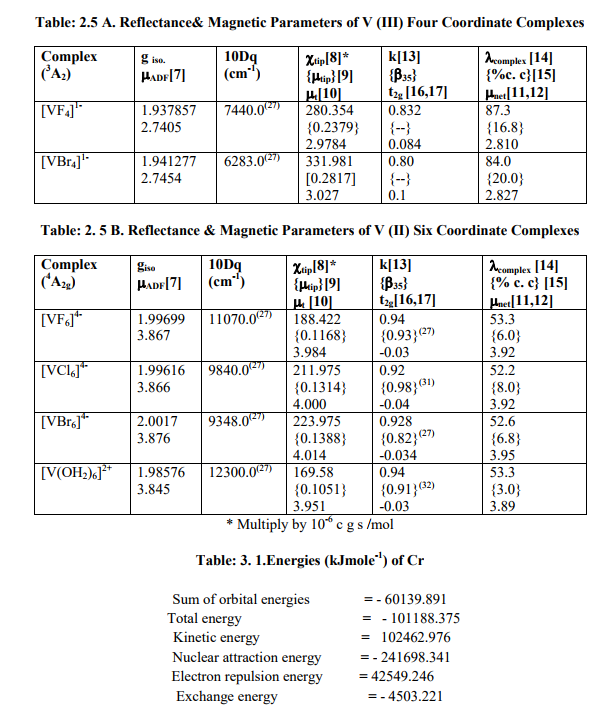
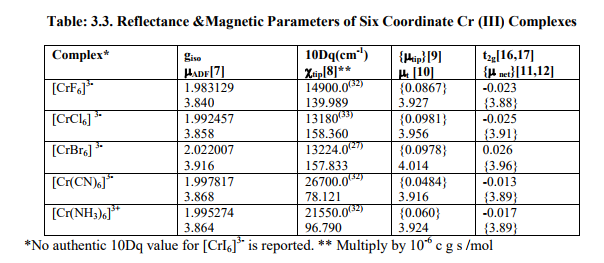
(D) Tables: 2.5-2.5B and 3.3 contain magnetic parameters of 7 out of the 13 V (II, III, IV) and 5 of the 6 Cr (III) complexes as calculated from their ESR and Reflectance parameters.

DISCUSSION

Calculation of ESR and NQR parameters [A]Effective Spin Hamiltonian (H^)

(a) The V (II, III, I V) complexes showed a variety of geometries .They were categorized as:

(i) [VX4] (X=F, Cl, Br, I) had D4h symmetry with (a) Two of the three g called g? had the same value and the third of higher value called g??. (b) Two of three a called a? parameters were of same value and third of higher value called a11. (c) Two of the three q values were same. (d) ?=0. Relation [2] was applied to calculate their H^.

(ii) [VX4] 1- (X=F, Cl, Br) were of regular Td symmetry with same values for g and a. Relation [3] was applied to calculate their H^.

(iii)[VI4] 1- had D4 h symmetry. Relation [2] was applied to calculate its H^.

(iv) [VX6] 4- (X= Cl, Br, I) and [VF 6] 4- were of Oh and D12 symmetries respectively with same g and a values. Relation [3] was applied to calculate their H^.

(v) [V (H2O) 6] 2+ had, no doubt, C1 symmetry but its g values were nearly the same. So relation [3] was applied to calculate its H^.

(b) The Six Cr (III) complexes showed either Oh or nearly Oh geometries and were categorized as:

(i) [CrX6] 3- (X= F, Cl, Br, I, CN) were of Oh symmetry with same g and a parameters. Relation [3] was applied to all to calculate their H^.

(ii) [Cr (NH3)6] 3+ had axial symmetry with (a) Two of the three g values called g? were same and the third of higher value called g?? . (b) Two of three a called a? parameters were of same value and third of higher value called a11. (c) Two of the three q values were of same value. (d) ? ? 0.Relation [2] wasapplied to calculate H^. (Put S_x=S_y=S_z=1/2, 1 and 3/2 for V(IV,III,II) ; I_x=I_y=I_z=3.5 ; g n= 1.4710588 and S_x=S_y=S_z=3/2; I_x=I_y=I_z=1.5 for Cr(III) ; gn= -0.3163600 ).

The contributions from four factors towards the total value of H^ for all the thirteen V (II, III, IV) and six Cr(III) complexes are given in small brackets of horizontal rows shown at the bottom of each complex (?) in Tables:2.2A- 2.4A and 3.2A respectively.

(c) Parameters such as (?), verification of Laplace equation (Tables: 2.1-2.3 and 3.2) and

(?E h f) (Tables: 2.1A- 2.3A and 3.2A) were calculated by relations 5, 6 and 4 respectively.

[B]Calculation of Reflectance and Magnetic parameters from ESR parameters (1) calculation of ?ADF , ?tip, ?tip , ?t , ?net , gt , t2g electron delocalization and its constant (k), ? complex and % covalent character(26) of V (II,III,IV) complexes.

(a) As the authentic 10Dq values of [VX4] (X=F, Br, I), [VX4] 1- (X=Cl, I) and [VI6] 4- were not reported in literature, calculation of their magnetic parameters was omitted.

(b) Table: 2. 5 contained only one complex [VCl4] with V (IV) having 2E ground term. All the above named parameters were calculated by putting ?V (IV) = 250.0 cm-1 .

(c) Table: 2 .5 A contained complexes [VX4] 1- (X=F, Br) with ground term 3A2 for V (III). All the above named parameters were calculated by putting ?V (III) =105.0 cm-1 .

(d) Table: 2.5 B had complexes such as [VX6] 4- (X=F, Cl, Br) and [V (OH2)6] 2+ with ground term 4A2g for V (II). ?V (II) being small (56.7 cm-1 ), they would possess negligibly small values of t2g electron delocalization. The parameter (k) was found to be reasonably in agreement with Nephelauxetic Ratio (?35) for these complexes (27, 31-32)

(2) Calculation of ?ADF, ?tip, ?tip, ?t, t2g electron delocalization, ?net for Cr(III) complexes (Table:3.3)

The constant (k) and ? Complex could not be calculated as 10 D q values of octahedral Cr (III) complexes were very high while ? Cr(III) [92.0 cm- 1 ] was small. So ?tip and t2g electron delocalization would be very small [ ? 2-4 % and ? 1-2 % of ?ADF respectively]. Lastly, in V (III), Cr (III) and V (IV) complexes, ?net values are expected to be somewhat less than their respective spin only (?so) values both in Td and Oh geometries. But very minor differences occur because as the charge increases (+3, +4), covalence increases (Fazans' rule) and crystal field approximations become poorer. Therefore, calculated parameters differ slightly from the experimental values. Also, assuming t2g electron delocalization to be equal to the average negative of difference of g t and g iso may not be an ideal assumption.

CONCLUSIONS With certain commands, the ADF software gave five ESR and NQR parameters. These parameters were used to calculate nine other ESR, NQR, Reflectance and Magnetic parameters by the selective use of 18 relations. So these 14 parameters of the four techniques were correlated in 36 Ti (II, III), V (II, III, IV) and Cr (III) complexes. Theoretically calculated values of these parameters were found to be fairly in agreement with their experimental values reported in the literature. The authors had already proved this fact in 20 Co (II) and Ni (II) complexes(1) in the previous communication and hope to prove the same in forty five more complexes of 2nd and 3rd transition series metal ions in the forthcoming communication.

ACKNOWLEDGEMENTS Authors acknowledge the immense help received from the scholars whose articles are cited and included in references of this manuscript. The authors are also grateful to authors/ editors/ publishers of all those articles, journals and books from where the literature for this article has been reviewed and discussed. Authors are grateful to Mr. S.R. Heer, Chief Engineer (Retd.), North Zone, Doordarshan, New Delhi (India), for his invaluable cooperation in the installation and smooth working of the ADF software.

References:

1. Harminder Singh, Bhardwaj, A.K.,Sehgal, M.L.and Susheel K.Mittal, IJCRR., 4[22](2012)12-28.

2. Atanasov, M., Daul, C. A. and Penka Fowe, E., Monatshefte für Chemie., 136 (2005)925-63.

3. Atanasov, M. and Daul, C.A., Chimia., 59(2005)504-10.

4. Pedersen,E. and Toftlund , H., Inorg.Chem.,13(1974)1603.

5. Urbach,F., J. Amer.Chem. Soc., 98 (1976) 5144 .

6. Mcgarvey, B.R., Can. J.Chem., 53 (1975) 2498.

7. Malatesta V. and Mcgravey B.R., Can. J. Chem.,53(1975)3791.

8. Reuvani, A., Malatesta. V. and Mcgarvey, B. R., Can J.Chem., 55 (1977)70 .

9. Hastey E., Colburn T.J. and Hendrickon, D.N., Inorg.Chem., 12(1973)2414.

10. Van Lanthe. E, vander Aroird and Wormer, P.E.S., J.Chem.Phys., 107(1997)2488-98.

11. Van Lanthe. E, vander Aroird and Wormer, P.E.S., J.Chem.Phys., 108(1998)783-96.

12. Van Lanthe.E. and Baerends, J., J.Chem. Phys., 108 (2000) 8279- 92.

13. Wulfsberg Gary, P., “Nuclear Quadrupole Resonance (NQR) Spectroscopy,” Online (2011)

14. Sathyanarayana D.N., “Introduction to Magnetic Resonance Spectroscopy ESR, NMR, NQR” (2009) Amazon.com .

15. Orgel. L. E.,“ Transition Metal Chemistry,’’ (1966) ; Methuen, London.

16. Tanabe, Y. and Sugano, S., J. Phys. Soc. Japan, 39(1954)753, 766.

17. Figgis B.N.,“Introduction to Ligand Fields, p.265 -66 ; 276-77(1966) ” Inter science , N.Y.

18. Ballhausen, C.J.,“Introduction to Ligand Field Theory,”(1962) ;McGraw-Hill, N.Y.

19. Cotton F.A. etal., J. Am. Chem. Soc., 83(1961) 4161 and references therein.

20. Leslie K.A., Drago, R.S., Stucky,G.D., Kitko, D. J.and Breeese, J.A.,Inorg. Chem.,18(1979) 1885.

21. Schoenherr, T., Atanasov, M. and Schmidtke, H., Inorg. Chim. Acta., 141(1988)27-32.

22. Gruen, D.M. and Mcbeth, R.L, Nature, 194(1962)468.

23. Fowles, G.W.A., Hoodless, R.A. and Walton, R.A., J. Inorg and Nuc. Chem., 27(1965) 391.

24. Baerends, E. J., Branchadel, V. and Sodup, e,., Chem. Phys. Lett., 265(1997) 481.

25. Lipkowitz, K. B. and Boyd, D. B., "KohnSham Density Functional Theory: Predicting and Understanding Chemistry" in Rev. Comput. Chem., p.1-86, Vol.15 (2000) Wiley-VCH, N.Y.

26. Atanasov, M., Daul, C.A. and Rauzy, C., Chem.Phys.Lett.,367( 2003)737-46.

27. Jorgensen C. K.,“Absorption Spectra and Chemical Bonding in Complexes,”(1962) Pergamon Press, N .Y.

28. Kilty P.A. and Nicholls, D., J. Chem. Soc., (1965) 4915.

29. Bedon, H.D., Horner, S.M. and Tyree, S.Y., J; Inorg . Chem., 4 (1965)743.

30. Blankenship, F. A. and Linn Belford, R., J. Chem. Phys., 36 (1962) 633.

31. Gruen D. M. and Mcbeth R. , Proc.7th I.C.C.C., Stocklholm,p.23.

32. Jorgensen, C. K., Advn. Chem. Phys., 5(1963)33.

33. Hatfield W. E., Fay R.C., Pfluger C.E. and Piper T. S., J. Am .Chem.Soc.,85 (1963)265.

34. Wood D.L., Ferguson, J., Knox ,K. and Dillon Jr. J.F., J.Chem.Soc.,85(1963) 265.

35. Meak D.W., Drago, R. S. and Piper, T.S., Inorg.Chem ., 1(1962)285.

36. Adamson A. and Dunn ,T. M., J .Mol. Spectroscopy., 18 (1965) 83.

37. Wentworth,R.A.D. and Piper, T.S., Inorg. Chem., 4 (1965) 709.

38. Bull W.E. and Ziegler, R.G., Inorg. Chem., 5(1966) 689.

39. Koch, W., Hotthausen, M., “A Chemist’s Guide to Density Functional Theory,” WileyVCH Weinheim, 2001.