IJCRR

IJCRR - 7(11), June, 2015

Pages: 65-69

Print Article   Download XML  Download PDF

EVALUATION OF PARAMETRIC TECHNIQUE OF TECHNICAL EFFICIENCY MEASUREMENT: APPLICATION TO SMALLHOLDER COTTON FARMERS IN ZAMFARA STATE, NIGERIA

Author: Odedokun V.O., Ahmed B., Omolehin R.A.and Atala T.K.

Category: Healthcare

Abstract:The focus of this Study is on evaluation of parametric technique of technical efficiency of smallholder cotton farmers in Zamfara state, Nigeria. The aims of the study were centred on estimation of the level of technical efficiency, inputs and output relationship and to determine elasticity and returns to scale in cotton production. Zamfara state was used for this study. The field survey employed the list from reconnaissance survey of farmers conducted by Zamfara State Agricultural Development Project ZADP. A multistage sampling technique was used in selecting the study farmers consisting 220 farmers who produce cotton. The average technical efficiency score was 0.67 implying that farmers can still maximise the utilisation of inputs and increase their production frontier by 33%. The input-output analysis showed that the average yield of cotton produced was 773.319kg/ha. The returns to scale (RTS) was 0.791 depicting a positive decreasing returns to scale and at stage (II) of the production function while The coefficients of all variable inputs were inelastic since the coefficient of regression with respect to each input employed, holding all other inputs fixed resulted in less than 1% increase in cotton output.

Keywords: Parametric, Technical Efficiency, Smallholder, Cotton Farmers, Nigeria

Full Text:

INTRODUCTION

At independence, the contribution of agri culture to the GDP was about 25% between 1975 and 1977. This was partly due to the phenomenal growth of the mining and partly as a result of the disincentives created by macroeconomic environment. Similarly, the growth rate of agricultural productivity exhibited a downward trend during the period. Thus, between 1970 and 1982 agricultural productivity stagnated at less than one percent annual growth rate at a time when the population growth rate was 2.5 to 3.0% per annum (Adubi, 2001). According to the National Bureau of Statistics (NBS) (2011), the percent share in the GDP of the crop sub-sector between 1981 to 1990 had been fluctuating between 28.37% and 22.99% and did not register any significant increase. This trend continued as the contribution of the crop sub-sector was almost stagnant at about 36% from 1994 to 1997 and from 2003 to 2006. With respect to cotton production trend had not witnessed remarkable improvement between 2007/2008 cropping year while the 2010 – 2012 cropping seasons experienced a decline. (USDA, 2011). . Batterham (2000) asserted that supply is yet to satisfy the level of demand for cotton. This is as result of low productivity and low efficiency of resource utilisation among cotton farmers. There are a number of factors affecting the productivity of farmers such as age, cropping patterns, years of farming experience, and lack of access to credit which tend to impact negatively on productivity and efficiency. Despite all human and material resources devoted to Nigerian agriculture, the productive efficiency of farmers for most crops still fall below 60%. The inefficiency problem is attributed to factors such as use of low input technologies, lack of knowledge of high input technologies and poor farm management skills, poor extension services, unavailability and high cost of inputs ( Obasi, 2005; Anyanwu and Obasi, 2010a; Anyanwu and Obasi, 2010b). This has caused great concern in the textile cotton fibre supply situation in the local market and export profile in the country thereby having a declining effect in its contribution to the agricultural economy of the country. It is with respect to this that cotton was chosen to form the basis of this study.

Research Question and Objectives

It is based on this credence that the following research questions and objectives were addressed by this study:

i. What is the level of technical, efficiency in cotton production in the state?

ii. What is inputs and output relationship in cotton production?

iii. What is the elasticity and returns to scale in cotton production?

The specific objectives of the study are:

i. To estimate the level of technical efficiency in cotton production;

ii. To estimate inputs and output relationship in cotton production;

iii. To determine elasticity and the returns to scale in cotton production.

Test of Hypotheses

i. Cotton farmers are not technically, allocatively and economically efficient in cotton production in the study area.

ii. There is no significant relationship between socioeconomic characteristics of farmers a n d the technical, allocative and economic efficiencies in the study area.

METHODOLOGY

Zamfara state was used for this study. The state lies between latitude 100 50`N and 130 38`N and longitudes 4o 16`E and 7o 18`E. The state is located in the Sudan Savanna ecological zone of Nigeria. It has a land area of 39,762km2 . Zamfara state shares common borders with Sokoto and the Republic of Niger to the north, Katsina and Kaduna states to the east, Niger and Kebbi states in the South (Yakubu, 2005., www.zamfarastate.net, 2010). The state has a population of about 3,259,846 people in 2006 according to the National Population Commission (NPC; 2006). This is projected in 2011 to be 3,667,326 People representing 3.2% annual growth rate in population. (UNFPA) (2013). The climate is essentially that of tropical climate. The rains usually commence in May/ June and end in September/October. The effective rainy season in the study area is restricted to July to mid September (Yakubu, 2005). Four local government areas namely Kaura, Gusau, Tsafe and Bungudu were randomly selected. A significant proportion of cotton produced in Zamfara state come from these areas (www.zamfarastate.net. 2010). The main ethnic groups in these areas are Hausas, Beriberis, Buzzaye and Fulanis. Indeed, agriculture forms the main occupation of the entire population. This constitutes the bulk of those involved in traditional farming, fishing, hunting and nomadic pastoralism. Sampling Procedures and Sample Size The field survey employed the list from reconnaissance survey of farmers conducted by Zamfara State Agricultural Development Project (ZADP, 2010). A multistage sampling technique was employed in selecting the study farmers. The first stage was random sampling of four local government areas (LGA’s). These are Kaura, Gusau, Tsafe and Bungudu. The second stage involve random selection of two villages known to be cotton growers from each of the local government areas based on the prevalence of cotton farmers and their involvement in cotton production and accessibility. Hence, a total of eight villages were selected for the study. The third stage involved using the list of cotton growers obtained from the reconnaissance survey to randomly select 15% of farmers from each of the eight villages in the ratio of 26, 33, 23, 26, 33, 22, 31 and 26 from KasuwaDaji, Kabarawa, Danba, Magami, Tsafe, Kucheri, Kwatarkwashi and Tashar-rawaya respectively constituting 220 out of a total of 1471 farmers. Primary data were used for this study. The primary data was collected for the study based on 2012/2013 cropping year known as cross-sectional data. The analytical tools that were used to achieve the stated objectives in this study were descriptive statistics and Stochastic Frontier Analysis.

Stochastic Frontier Models

This technique was used to achieve the stated objectives of the study. The Stochastic Frontier Approach (SFA) is parametric which uses econometric method employing the production function of Cobb-Douglas form. It is one of the methods for estimating frontier functions in efficiency of production. Using the SFA, it is suitable to test hypothesis to ascertain whether the cotton production enterprises were technically efficient or not. This approach was taken up by Aigner and others which subsequently resulted in the development of this method in econometric studies. Aigner and Chu (1968), Aigner et al (1977) and Van de Broeck (1979) considered the estimation of a parametric frontier production function which was later improved and applied by Battese and Coelli (1995). The Stochastic frontier production function model is specified as:

This Vi ’s are random variables which account for random variation in output due to factors outside farmers control such as weather, disease and measurement error in production. The random error (Vi ’s) are assumed to be independently and identically distributed N(σ2 v) and independent of . It constitutes noise or disturbance error (Vi ’s). The Ui ’s are random variables that account for technical inefficiency of the farm as reflected in the socio-economic characteristics and other variables within farmers’ control. The Ui ’s are assumed to be non-negative truncation of the half-normal distribution N(σ2 U).

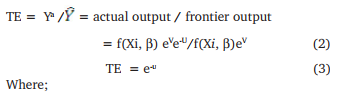
TE = Technical efficiency, X1 = Farm size (ha), X2 = Seed (kg/ha), X3 = Family labour (man-days/ha), X4 = Hired labour (man-days/ha), X5 = Fertilizer (kg/ha), X6 = Agro-chemicals (liter/ha), β1 – β6 = vector parameters to be estimated, βo = Intercept term, ei = Vi – Ui (Composite error term)

This is the technical efficiency which is defined as the ratio of observed output to maximum feasible output which is called frontier output. The empirical stochastic frontier was specified by Cobb-Douglas production function by taking the logarithm form, the model can be written as;

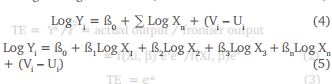
When TEi = 1 it shows that a farm obtains the maximum feasible output while TEi < 1 provides measures of shortfall of the observed output from the frontier output. In this study, the production function specified in equation (5) above is amenable, tractable and compatible by been transformed in its logarithm form. According to Coelli (1995), a logarithmic transformation provides a model which is linear in the log of inputs and hence, easily used in econometric estimation. Aigner et al. (1977) and Meeusen and Van den Broeck (1977) independently proposed the stochastic frontier production function in which an additional random error Vi is added to the nonnegative random variable Ui. Its most attractive feature is its simplicity.

RESULTS AND DISCUSSION

Estimation of Technical Efficiency Indices among Cotton Farmers

This section deals with the stochastic frontier analysis as a parametric method that computes the parameter estimates. This is by iteratively maximizing a non-linear function of the unknown parameters in the model subject to the constraints. Ajibefun (2008), highlights parametric methods to include production, cost, profit and revenue functions as alternative methods of describing the production technology and estimating efficiency of production. Table 1 shows the frequency distribution of technical efficiency indices in cotton production. The minimum technical efficiency was 0.11 while the maximum technical efficiency score index was 0.97 with a mean technical efficiency score index of 0.67. This implies that farmers could increase their level of output by improving on their efficiency index of input allocation and utilization through adoption of recommended technological packages by 0.33.

In a similar study by Adzawla et al., (2013) in estimating technical efficiency of cotton production in Yendi Municipality, Northern Ghana, it was reported that the average technical efficiency level of 0.88, ranging from

0.70 and 0.99 were observed. This is comparable to that of many studies (Mohammed Yusuf, 2005; Tsimpo, 2010; Neba et al., 2010). The wide difference in technical efficiency among least practice and best practice farmer indicates an opportunity for efficiency improvement. Input-output Relationship in Cotton Production The result of the Stochastic Frontier Production Function showed that the estimated coefficients for most inputs were positive except for family labour and hired labour which were negative. Farm size and family labour were significant at 1% level of significance. The insignificance of hired labour may be attributed to the use of family labour by cotton famers as substitutes for hired labour. (Table 2).

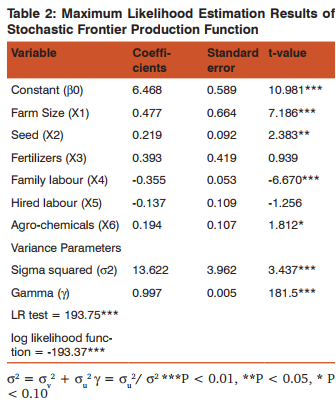
This implies that increase in farm size and family labour would result to an increase in output level in cotton production in the study area. The coefficient of seed input was observed to be positive and significant at 5% level of probability. By implication, there exists a direct relationship between seed and cotton output produced by farmers. Hired labour input and family labour were negative in terms of their coefficients and the t-value was insignificant with respect to hired labour. This implies that hired labour input does not have any meaningful influence on the level of output in cotton production. Family labour was significant at 1% level of significance. Contrary to the a priori expectation, family labour cost had a negative and significant coefficient.

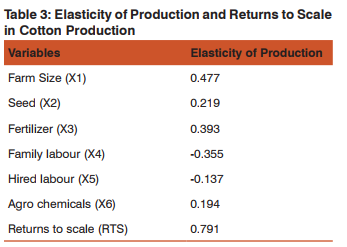
Elasticity of production and returns to scale

The coefficients of all variable inputs were inelastic since the coefficient of regression with respect to each input employed, holding all other inputs fixed resulted in less than 1% increase in cotton output. The sum of the elasticities derived from Cobb-Douglas equation was 0.791. This depicts that when all inputs were increased by 1% the output will increase by 0.79% showing that resources employed in cotton production were inelastic. The equation exhibits a positive decreasing returns to scale in stage II where every farmer strives to attain to maximize profit and minimize cost of production. (Table 3). 

Test of hypothesis on technical efficiency model (Ho1)

Estimates of the parameters of the technical efficiency model are statistically significant with the null hypothesis that . The likelihood ratio test of hypothesis for parameters of production function model revealed that farmers were technically efficient in cotton production in the study area. The value of the likelihood ratio test statistic shown in table 4 is 193.75 which is far more than the critical t-value of 2.40 at 0.01 level of probabilities. Hence, the decision is to reject the null hypothesis Ho 

The result of test of hypothesis on the stochastic frontier efficiency and inefficiency models imply that most of the variables had meaningful and direct bearing on farmer’s productivity and efficiency. This outcome may

be required by farmers, agro-service agencies and government when planning for production and investment in the cotton production industry.

CONCLUSION AND RECOMMENDATIONS

The results of the stochastic frontier analysis showed that the technical efficiency involved in cotton production was above average and farmers can still improve on them. Cotton production function exhibits positive decreasing returns to scale with inelastic response of variable inputs to the level output produced. It is on this basis that the following recommendations were proffered: i. Improved access to inputs required in production which are pre-requisite for adoption and use of improved recommended cotton production practices are proffered ii. Adequate and intensive research and extension programme are required to disseminate improved and recommended cotton production technological packages to farmers. iii. Adoption and use of appropriate recommended cotton production practices to enhance high yields through adequate implementation as a package are recommended.

ACKNOWLEDGEMENT

Authors acknowledge the immense help received from the scholars whose articles are cited and included in references of this manuscript. The authors are also grateful to authors / editors / publishers of all those articles, journals and books from where the literature for this article has been reviewed and discussed.

References:

1. Adubi, A. A. (2001). Agriculture in the Nigerian Economy. Being a Paper Presented At the Workshop on Planning and Management of Agriculture Sector, August 14 – 25, Organized by Nigeria Centre for Economic Management. (NCEMA), Ibadan.

2. Adzawla, W., Fuseini, J., and Donkoh, S.A. (2013). Estimating Technical Efficiency of Cotton Production in Yendi Municipality, Northern Ghana. Journal of Agriculture and Sustainability. 4: 115-140.

3. Aigner, D. J., and Chu, S. F. (1968). “On Estimating the Industry Production Function”. American Economic Review, 58, 826-839.

4. Aigner, D. J., Lovell, C. A. K. and Schmidt, P. (1977). Formulation and Estimation of Stochastic Frontier Production Function Models. Journal of Econometrics. 6. 21-37.

5. Ajibefun, I.A. (2008). An Evaluation of Parametric and Non-parametric Methods of Technical Efficiency Measurement: Application to Small Scale Group Production in Nigeria. Journal of Agricultural Sc; 4:95 -100

. 6. Anyanwu, S.O. and Obasi P. C.(2010a) ,Comparative Analysis of Land Productivities in low and High External Input Technology Agriculture in Imo State, Nigeria. Acta Agronomica Nigeriana. 10(1):15–21.

7. Anyanwu, S.O. and Obasi P.C. (2010b) Comparative Analysis of Aggregate Agricultural Productivity Between Low and High External Input Technology Farms in Nigeria. African Journal of Biotechnology. 9(34):5530–5534

. 8. Batterham, R. (2000). The Chance to Change. Discussion Paper by the Chief Scientist Camberra, African Summit, Abuja, Nigeria

. 9. Battese, G. E. and Corra, G. S. (1977). Estimation of a Production Frontier Model; with Application to the Pastoral Zone of Eastern Australia. Australian Journal of Agricultural Economics, 21:167-179.

10. Coelli, T. J. (1996). A Guide to FRONTIER Version 4.1: A Computer Programme for Coulibaly, O. Mbila, D., Sonwa, D. J., Adesina, A. and Bakala, J. (2006); Integrated Pest Management Reviews. Springerlink Journal. 7(3) 165-175.

11. Meeusen, W. and Broeck van de, J. (1977). “Efficiency Estimation from Cobb-Douglas Production Functions with Composed Error”. International Economic Review, 18: 435- 444.

12. Mohammad-Yusuf, T. (2005). The Effects of Market Reforms on Cotton Production Efficiency. The case of Tajkistan. Asian Pacific School of Economics and Governments Working Paper 05-5.

13. National Bureau of Statistics (NBS). (2011). Nigeria Gross Domestic Product at 1990 Constant Basic Prices.

14. National Population Commision (NPC), (2006). ,Population Census of the Federal Republic of Nigeria. Analytical Report at the National Population commission, Abuja, Nigeria.

15. Neba, C., Ngassam, S. and Nzomo, J. (2010). The Determinants of the Technical Efficiency of Cotton Farmers in Northern Cameroon. MPRA Paper No. 24814.

16. Obasi, P. C. (2006). Application of Trans-log Function to Productivity Estimation in Imo State, Nigeria. International Journal of Agriculture and Rural Development (IJARD). 6:26–33.

17. United Nations Population Fund (UNFPA) (2013). Available on-line @http: Nigeria. unfpa.org/zamfara.html. Retrieved: 05/12/2013.

18. United State Department of Agriculture. (USDA) (2011). Nigeria Cotton Production by year. http://www.indexmundi.com Accessed, 02/09/2011.

19. Yakubu, A. A. (2005). Risk and Risk Management in Cotton Production among Farmers in Zamfara State, Nigeria. Unpublished M.Sc. Thesis Submitted to the Department of Agricultural Economics, Usman Dan Fodio University, Sokoto, Sokoto State, Nigeria. 20. ZADP (2010). Zamfara State Agricultural Development Project (ZADP) Reconnaissance Survey. 21. Zamfara State (2010). www.zamfarastate.net Accessed Jan. 2013.