IJCRR

IJCRR - 3(10), October, 2011

Pages: 127-135

Print Article   Download XML  Download PDF

PARTICLE SWARM OPTIMIZATION FROM A RESEARCH PERSPECTIVE

Author: T.V.Mahendiran, P.Thangam, K. Thanushkodi

Category: Technology

Abstract:The work is an outcome of the motivation caused by the increasing awareness of the need for innovative
PSO schemes featuring an appropriate methodology for optimization. PSO is a swarm intelligence-based
evolutionary algorithm inspired originally by the social behavior of bird flocking. PSO finds its
applications successfully in many areas including function optimization, neural network training, solving
multidimensional complex problems, fuzzy systems, etc. The simplicity of implementation and weak
dependence on the optimized model of PSO make it a popular tool for a wide range of optimization
problems. This paper consists of an overall review of the various PSO schemes and developments in the
literature. This review also recommends some research areas in this field, highlighting those leading to
high efficiency.

Keywords: PSO, bird flocking, convergence, Swarm intelligence, function optimization.

Full Text:

I. INTRODUCTION

Particle Swarm Optimization (PSO) is an algorithm for finding optimal regions of complex search space through interaction of individuals in a population of particles. PSO algorithm, originally introduced in terms of social and cognitive behavior by Eberhart and Kennedy in 1995 [1] has been proven to be a powerful competitor to other evolutionary algorithms such as genetic algorithms. PSO is a population based stochastic optimization technique and well adapted to the optimization of nonlinear functions in multidimensional space. PSO has received significant interest from researchers studying in different research areas and has been applied to several real-world problems. PSO algorithm simulates social behavior among individuals (particles) flying through multidimensional search space, each particle representing a single intersection of all search dimensions [2], [3]. The particles evaluate their positions relative to a global fitness at every iteration, and companion particles share memories of their best positions, and then use those memories to adjust their own velocities and positions.

II. BACKGROUND OF PSO PSO

incorporates swarming behaviors observed in flocks of birds, schools of fish or swarms of bees, and even human social behavior. It is a population-based optimization tool, which could be implemented and applied easily to solve PARTICLE SWARM OPTIMIZATION FROM A RESEARCH PERSPECTIVE T.V.Mahendiran1 , P.Thangam2 , K. Thanushkodi3 1EEE Department, Coimbatore Institute of Engineering and Technology, Coimbatore, Tamilnadu 2CSE Department, Sri Ramakrishna Engineering College, Coimbatore , Tamilnadu 3Akshaya College of Engineering and Technology, Coimbatore , Tamilnadu E-mail of Corresponding Author: saimahegobi@gmail.com International Journal of Current Research and Review www.ijcrr.com Vol. 03 issue 10 October 2011 128 various function optimization problems [4]. The main strength of PSO is its fast convergence than the other global optimization algorithms. PSO utilizes a population of candidate solutions to evolve an optimal or near-optimal solution to a problem [5]. The degree of optimality is measured by a fitness function defined by the user. PSO is similar to the evolutionary computation techniques such as Genetic Algorithms (GA), Evolutionary Programming (EP), Evolution Strategies (ES), and Genetic Programming (GP) in that the system is initialized with a population of random solutions and searches for optima by updating generations. PSO differs from the evolutionary computing methods in that the population members, called particles, fly through the problem space by following the current optimum particles. Each particle keeps track of its coordinates in the problem space which are associated with the best solution (fitness) it has achieved so far [6]. (The fitness value is also stored.) This value is called pbest. Another "best" value that is tracked by the particle swarm optimizer is the best value, obtained so far by any particle in the neighbors of the particle. This location is called lbest. When a particle takes all the population as its topological neighbors, the best value is a global best and is called gbest. The particle swarm optimization concept consists of, at each time step, changing the velocity of (accelerating) each particle toward its pbest and lbest locations (local version of PSO). Acceleration is weighted by a random term, with separate random numbers being generated for acceleration toward pbest and lbest locations.

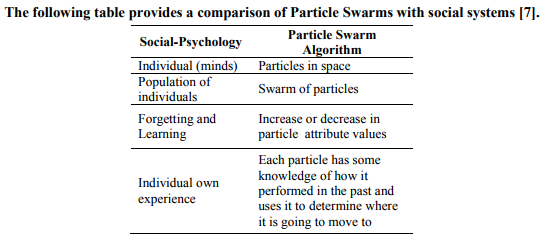
In past several years, PSO has been successfully applied in many research and application areas. It is demonstrated that PSO gets better results in a faster, cheaper way compared with other methods. Another reason that PSO is attractive is that there are few parameters to adjust. One version, with slight variations, works well in a wide variety of applications. Particle swarm optimization has been used for approaches that can be used across a wide range of applications, as well as for specific applications focused on a specific requirement.

III. DEVELOPMENTS OF PSO

A. Adaptive Mutation PSO (AMPSO) Zhen-Su, Zhi-Rong and Juan [8] presented a new adaptive mutation PSO, which is based on the variance of the population‘s fitness. During the running time, the mutation probability for the current best particle is determined by two factors: the variance of the population‘s fitness and the current optimal solution. The ability of PSO algorithm to break away from the local optimum is greatly improved by the mutation. The experimental results show that the new algorithm has great advantage of convergence property over traditional PSO and also avoids the premature convergence problem effectively.

B. Self-organization PSO (SOPSO) Jie, Zeng, and Han developed a selforganization PSO with the aim to alleviate the premature convergence [9]. SOPSO emphasizes the information interactions between the particle-lever and the swarmlever, and introduce feedback to simulate the function. Through the feedback information, the particles can perceive the swarm-lever state and adopt favorable behavior model to modify their behavior, which not only can modify the exploitation and the exploration of the algorithm adaptively, but also can vary the diversity of the swarm and contribute to a global optimum output in the swarm. Results show that SOPSO performs very well on benchmark problems, and outperforms the basic PSO in search ability.

C. Attractive and Repulsive PSO (ARPSO) Xuan and Jihong proposed Attractive and Repulsive PSO (ARPSO) [10]. It performs optimization using two phases. In attractive phase, particles converge to promise regions in the search space. In repulsive phase, particles are repelled each other along opposition directions. When the particles diversity is high, the particles will attract each other just as the basic PSO algorithm. The information of good solutions will flow between particles. When the particles diversity is low, it turns to repulsive phase, particles are no longer attracted to but instead are repelled and new potential particles are created. Premature convergence is avoided by the new potential particles. Experiments show that this method is feasible and robust.

D. Immune PSO (IPSO) In optimization processing of PSO, premature convergence often takes place especially for the case of uneven solution population distribution. Ying and Zhidong proposed a combination of an immune system and PSO to improve the diversity of particles and reduce the premature convergence [11]. Biological research on the immune system indicates that the immune principle can provide inspiration for the improvement of the performance of evolution computations. Inspired by the diversity of biological immune systems, a diversity retaining mechanism based on concentration and immune memory is introduced in the IPSO. Immune behavior is beneficial for retaining diversity, which can effectively avoid premature convergence and improve the search speed and quality of the algorithm.

E. Amnesia PSO (APSO) Amnesia PSO [11] algorithm makes use of an efficient mechanism to improve the diversity of particles and thereby reducing the premature convergence. The mechanism is called forgetfulness mechanism. The basic idea is that a slight amnesia is imposed on each particle and the swarm, when the particle swarm tends to premature convergence. Each particle forgets its historical best position and considers the current position as its best position. Similarly, the swarm does not remember its historical global best position and choose the best position from the current positions of all particles. This mechanism gives the particles a new chance based on existing better conditions. Thus this method turns out to be an effective solution to overcome the problem of premature convergence.

F. PSO based on informative Diffusion and Clonal Selection (InformPSO) Information diffusion among biological particles is a time process. Particles, close to the current best particle, change the direction and rate of velocities fleetly towards it, while particles, far from it, move more slowly towards it. On the assumption that information is diffused among particles in a short time, information received by particles close to the global best is more than that received by those far from it. Thus InformPSO [12], suggested by Li et. al, adjusts the variable ?social cognition‘ aspect of particles. This improves the local search ability of PSO, increases the particles‘ diversity and enables the swarm to overcome premature convergence problem.

G. Emotional PSO (EPSO) Ge and Rubo [13] presented a modification of the PSO, intended to introduce some psychology factor of emotion into the algorithm. In the new algorithm, which is based on a simple perception and emotion psychology model, each particle has its own feeling and reaction to the current position, and it also has specified emotional factor towards the sense it got from both its own history and other particles. All these psychology factors will influence the next action of the particle. This new algorithm outperforms PSO on four test functions, being less susceptible to premature convergence, and less likely to be stuck in local optima. EPSO algorithm outperforms the PSO even in its faster convergence speed.

H. Hybrid PSO (HPSO) Yang, Chen and Zhou presented a new hybrid algorithm of PSO called PSOSA [14] in which the mechanism of modified simulated annealing (SA) is embedded into standard PSO algorithm. When the optimal particle of particle swarm is got into local optimum, the particle swarm is very hard to jump out of the local optimum with standard PSO. The SA has the character of probability-sudden-jump so as to be able to jump out of the local optimum and approach the global optimum. The proposed Hybrid PSO merges these two different optimization mechanisms into a whole, which is in favor of enriching the search behavior during optimization process and enhancing the searching ability and efficiency in global and local. PSO enables SA to be parallel SA. Meanwhile, the SA enhances and complements the ability of PSO getting rid of local minimum, which avoid getting into local minimum and approach global minimum. This algorithm not only keeps the characters simple and easy to be implemented, but also enhances the ability of getting rid of local optimum and improves the speed and precision of convergence. The testing results of several benchmark functions with different dimensions show that the proposed HPSO algorithm is superior to standard PSO and other PSO algorithms.

I. Independent Neighborhoods PSO (INPSO) Grosan, Abraham, Han and Gelbukh proposed a novel hybrid PSO – evolutionary algorithm (INPSO) [15] for solving the well known geometric place problems. The proposed PSO algorithm is similar to the classical one, but which uses neighborhoods. Thus the particles fly in independent subswarms. It divides the swarm into multiple independent neighborhoods. The dimension of each neighborhood (sub-swarm) is the same for all considered sub-swarms. By considering different sub-swarms, the number of solutions, which can be obtained at the end of the search process, is at most equal to the number of sub-swarms. This INPSO algorithm is very fast compared to the evolutionary algorithms (EA). But, for difficult problems, there can be some particles, which could never converge. Taking into account these issues, a hybrid approach involving both INPSO and EA is developed. The key advantages of the hybrid approach are in making use of the fast convergence property of INPSO and EA‘s definite convergence. The combination obtains the solutions very fast and all individuals converged to the geometrical place with fewer iterations.

J. Discrete PSO (DPSO) DPSO [16] approach, motivated by swarm behavior, makes use of velocity and position to obtain the globally optimal partition of the data. Many researchers search for parameter values from incomplete data using Expectation Maximization (EM) algorithm. The EM algorithm is an iterative approach to compute maximum a posteriori and maximum likelihood parameters from incomplete data. EM approach has the drawback of local optimum solution because it is sensitive to initialization. The DPSO method is an evolutionary method to estimate conditional probabilities from incomplete data sets. DPSO method has strong global search ability and parallel performance, but the convergence rate of the DPSO algorithm is painfully slow. So Guan and Liu proposed a novel hybrid algorithm as a combination of DPSO and the EM approach to improve the global search performance. The DPSO+EM method overcomes the disadvantages of these two approaches by performing a local optimization using the EM method at each particle. The approach is applied to 4 realworld data sets and the results show that the hybrid DPSO+EM algorithm exhibits more efficiency and outperforms the EM approach.

K. Fuzzy PSO (FPSO) Yi, Yao and Jiang presented a fuzzy PSO method [17] and applied it to image clustering. In this method, particles search the International Journal of Current Research and Review www.ijcrr.com Vol. 03 issue 10 October 2011 132 optimal cluster centers in solution space, and images are classified according to the membership degree of images to cluster centers. First the fuzzy concept is combined with the PSO algorithm. Second, to solve the ?curse of dimensionality‘ problem, feature weights are introduced, which are dynamically determined during clustering, to represent the importance of features. Image classification and clustering is a challenging problem in computer vision. The fuzzy PSO approach considers each particle as a cluster center. The particles fly in the solution space to search suitable cluster centers. This method is different from previous work in that it employs fuzzy concept in PSO and adopts attribute selection mechanism to avoid the ?curse of dimensionality‘ problem. The experimental results show that the presented approach can properly process image clustering problem. Future extension is to improve the speed of the algorithm.

L. Multi-objective PSO (MOPSO) Luis, Noel and Carlos [18] proposed a new multi-objective evolutionary algorithm, which consists of a hybrid between PSO and scatter search. The main idea of the approach is to combine the high convergence rate of the PSO algorithm with a local search approach based on scatter search. A new leader selection scheme is proposed for PSO, which aims to accelerate convergence. Upon applying PSO, scatter search acts as a local search scheme, improving the spread of the non-dominated solutions found so far. Thus, the hybrid constitutes an efficient multiobjective evolutionary algorithm, which can produce reasonably good approximations of multi-objective problems of high dimensionality. The proposed approach is validated using ten standard test functions.

IV.ANALYSIS OF PSO SYSTEM 4.1 Advantages of PSO The reasons for why PSO replaces the other evolutionary computing algorithms are as follows:

• With a population of candidate solutions, a PSO algorithm can maintain useful information about characteristics of the environment.
• PSO, as characterized by its fast convergence behavior, has an in-built ability to adapt to a changing environment.
• Some early works on PSO have shown that PSO is effective for locating and tracking optima in both static and dynamic environments

4.2 Applications of PSO PSO finds its applications in the following areas: Evolving neural networks, Human tumor analysis, Computer numerically controlled milling optimization, Battery pack state-ofcharge estimation, Real-time training of neural networks, Servomechanism, Reactive power and voltage control, Ingredient mix optimization, Moving Peaks (multiple peaks dynamic environment), PSO can be tailor-designed to deal with specific real-world problems.

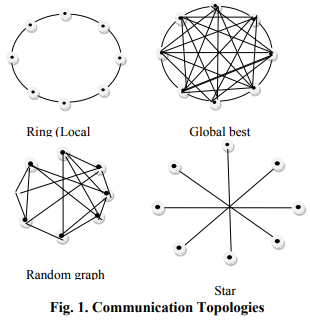
4.3 Parameters that affect the performance of PSO The performance of the PSO algorithm depends largely on the following parameters [19]: 1)Initialization methods, 2)Population size, 3)Population diameter, 4)Absolute vs. signed velocities, 5)Population topology, 6)Births, deaths, migration, 7)Limiting domain, 8)Multiobjective optimization techniques, 9)Comparison over problem spaces, and 10)Hybrids. Of the above mentioned parameters, topology plays a vital role. It determines how the solutions spread through the population, and hence affects the rate of convergence and parallelism of the search. This is illustrated as follows:

• gbest: each particle is influenced by the best found from the entire swarm. ?
• lbest: each particle is influenced only by particles in local neighborhood. Some of the topologies commonly adopted in PSO are depicted in Fig 1. Some latest innovations in topologies include mean degree, dynamic clustering, heterogeneity, etc. The choice of the best suitable topology for the current problem improves the performance of the PSO algorithm. Thus, there should be a good balance between exploration and exploitation, (i.e.) gbest model propagate information the fastest in the population; while the lbest model using a ring structure the slowest. For complex multimodal functions, propagating information the fastest might not be desirable. However, if this is too slow, then it might incur higher computational cost. Mendes and Kennedy [20] found that von Neumann topology (North, South, East and West, of each particle placed on a 2 dimensional lattice) seems to be an overall winner among many different communication topologies.

4.3 Future analysis of PSO We have already discussed the parameters that affect the performance of a PSO system. The other future analyses on the PSO [21] are: Trajectory analysis, Interaction Analysis, Probability Distribution Analysis. These analyses could be conducted for better learning about the swarm thus promoting excellent swarm behaviors.

V. RESEARCH AND

RECOMMENDATIONS

Robustness of a PSO algorithm can be determined by several factors. They include: Quality of the algorithm, Search speed, Search ability , Diversity of particles, Property of convergence, and accuracy. Thus, a PSO algorithm can be chosen to solve a particular problem by considering the requirements in terms of convergence, search and ultimately the quality and efficiency of the algorithm. The factors to be considered when choosing a Ring (Local best) Global best Random graph Star International Journal of Current Research and Review www.ijcrr.com Vol. 03 issue 10 October 2011 134 particular variant and/or a parameter set [22] are: characteristics of the problem, available search time, and the solution quality threshold. A number of research directions are currently pursued, to name a few: Matching algorithms, application to different kind of problems, parameter selection, identification of ?state-ofthe-art? PSO algorithms, new variants, and theoretical aspects.

VI.CONCLUSIONS The paper presents a survey of literature on Particle Swarm Optimization. The different types of PSO algorithms are reviewed and classified based on properties such as their search ability, immunity to premature convergence and also the fundamental methodology used. The advantages of PSO are highlighted and also the applications of PSO in diverse areas are discussed. An analysis is performed on the PSO system, identifying parameters that affect the performance of the system. Some future analysis and recommendations are provided. Also, based on the review, the proposal on the ways of detecting a robust PSO algorithm is presented. Finally, the research directions in this area are discussed with further recommendations.

References:

1. J. Kennedy, and R.C. Eberhart, ?Particle Swarm Optimization,? Proc of the IEEE International Conference on Neural Networks, Australia, pp. 1942–1948. 1995.

2. http://www.swarmintelligence.org/

3. http://www.particleswarm.info/

4. Nadia Nedjah, Luiza de Macedo Mourelle, Swarm Intelligent Systems, Springer, 2006.

5. J. Kennedy, R.C.Eberhart, Y.Shi, Swarm Intelligence, Morgan Kaufmann Publishers, 2001.

6. R.C.Eberhart, and Y.Shi, ?PSO: Developments, Applications and Resources?, IEEE conference, 2001.

7. Riccardo Poli, James Kennedy, Tim Blackwell, Particle swarm optimization. Swarm Intelligence, 1(1): 33-57, 2007.

8. Lu Zhen-Su, Hou Zhi-rong, and Du Juan, ?Particle Swarm Optimization with Adaptive Mutation,? Springer-Verlag, pp. 99-104, 2006.

9. Jing Jie, Jianchao Zeng, and Chongzhao Han, ?Self-Organization Particle Swarm Optimization based on Information Feedback,? Springer-Verlag, LNCS 4221, pp. 913-922, 2006.

10. Yang Xuan, and Pei Jihong, ?Elastic Image Registration using Attractive and Repulsive Particle Swarm Optimization,” SpringerVerlag, LNCS 4247, pp. 782-789, 2006.

11. Li Ying, and Deng Zhidong, ?Multiresolution Neural Networks based on Immune Particle Swarm Optimization,? Springer-Verlag, LNCS 4221, pp. 97-106, 2006.

12. Yamping Li, Shaozi Li, Shuili Chen, Qingshen Jiang, and Wenzhong Guo, ?Particle Swarm Optimization Based on Information Diffusion and Clonal Selection,? Springer-Verlag, LNCS 4247, pp.521-528, 2006.

13. Yang Ge, and Zhang Rubo, ?An Emotional Particle Swarm Optimization Algorithm,? Springer-Verlag, LNCS 3612, pp. 553-561, 2005.

14. Guangyou Yang, Dingfang Chen, and Guozhu Zhou, ?A new hybrid algorithm of Particle Swarm Optimization,? SpringerVerlag, LNBI 4115, pp. 50-60, 2006.

15. Crina Grosan, Ajith Abraham, Sangyong Han, and Alexander Gelbukh, ?Hybrid Particle Swarm-Evolutionary Algorithm for Search and Optimization,? Springer-Verlag, LNAI 3789, pp. 623-632, 2005. International Journal of Current Research and Review www.ijcrr.com Vol. 03 issue 10 October 2011 135

16. Jing-Hua Guan, Da-You Liu, and Si-Pei Liu, ?Discrete Particle Swarm Optimization and EM Hybrid Approach for Naïve Bayes Clustering,? Springer-Verlag, LNCS 4233, pp. 1164-1173, 2006.

17. Wensheng Yi, Min Yao, and Zhiwei Jiang, ?Fuzzy Particle Swarm Optimization Clustering and Its Application to Image Clustering,? Springer-Verlag, LNCS 4261, pp. 459-467, 2006.

18. Luis V. Santana-Quintero, Noel Ramirez, and Carlos Coello, ?A Multi Objective Particle Swarm Optimizer Hybridized with Scatter Search,” Springer-Verlag, LNAI 4293, pp. 294-304, 2006.

19. J.Kennedy, R.Eberhart, ?Tutorial on Particle Swarm Optimization?, IEEE Swarm Intelligence Symposium 2005, USA, 2005.

20. Kennedy, J., and Mendes, R., ?Population structure and Particle Swarm Performance?, Proc. of the 2002 World Congress on Computational Intelligence, 2002.

21. Xiaodong Li, Particle Swarm Optimization: An introduction and its recent developments, A tutorial prepared for SEAL‘06, 2006.

22. Marco A. Montes de Oca, Universit´e Libre de Bruxelles (U.L.B.), Particle Swarm Optimization: Introduction, 2007.