IJCRR

IJCRR - 4(18), September, 2012

Pages: 148-153

Date of Publication: 29-Sep-2012

PERFORMANCE OF DFT FOR THE CALCULATION OF HYPERFINE COUPLING CONSTANTS OF SOME ISOTROPIC METAL COMPLEXES

Author: P.L.Verma, Vinita Prajapati, Dhirendra Prajapati

Category: General Sciences

Abstract:The performance of DFT methodology to predict with accuracy the hyperfine coupling constants (hfccs) of isotropic metal complex, [Mn(CN)4N]- [Cr(CO)4]+,and Co (CO)4] have been investigated. For this investigation, , BHPW91, B3LYP, B3PW91, BLYP, BHLYP,BPW91, BP86, BHP86 functionals have been used. The hyperfine coupling constants values obtained from different density functionals have been found in the order of BHPW91> BHP86 > BHLYP > BLYP > BP86> BPW91> B3LYP > B3PW91 >EXP for [Mn(CN)4]2- , BLYP >BP86 >BPW91>B3LYP >B3PW91> BHLYP >BHP86 >BHPW91 >EXP for [Cr(CO)4]+ and BHPW91> BHP86> BHLYP> BLYP > BP86 > BPW91> B3PW91> B3LYP >EXP for [Co (CO)4]. The performance of the functional B3PW91 has been found better for Isotropic Metal Complexe [Mn(CN)4N]- ,BHPW91 for Isotropic Metal Complex [Cr(CO)4] and B3LYP for Isotropic Metal Complexe [Co (CO)4]. We have inferred that results obtained by DFT calculated EPR parameter hyperfine coupling constant values are in close agreement with experimentally observed values.

Keywords: Density Functional Theory (DFT). Isotropic Metal Complexes, Hyperfine coupling Constant.

Full Text:

INTRODUCTION
Experimental method based on electron paramagnetic resonance phenomena belongs to most widely experimental techniques for investigation of molecular and electronic structure the difficulty with such experiments usually a proper interpretation of data obtained from high resolution spectra, opens new challenges for pure theoretical methods. One of these methods is density functional theory that now has an advanced position among the whole variety of computational techniques [11,12]. The computation of the structure of transition metal complexes has been an area of long standing interest, with clear problems not present in the corresponding studies of 1st and 2nd row species [5].Much of the growing acceptance by the physics and chemistry community of Density Functional Theory (DFT) is due to its success in treating transition metal complexes, in stark contrast to the failure of the Hartree Fock method. This technique presently the most successful approach to compute electronic structure of matter and hence for calculation of EPR parameters such as g-tensors and hyperfine coupling constants A of transition metal complexes [6, 22]. The basic idea behind DFT is to use the electron density rather than the quantum mechanical wave function to obtain information about atomic and molecular systems. While this idea came up in the very.

first years of quantum mechanics with the pioneering work of Thomas and Fermi in 1927[9] and was continued with Slater [24] the Hohenberg-Kohn theorems [7] are regarded as the real beginning of DFT. The most fundamental of these approaches originates from the pioneering work of Hartree and Fock [20] .Modern DFT rests on two theorems by Hohenberg and Kohn [8,10] .The major problem of DFT: the exact functionals for exchange and correlation are not known except for the free electron gas. However, many approximations exist which permit the calculation of molecular properties at various levels of accuracy. The most fundamental and simplest approximation is the local-density approximation (LDA), in which the energy depends only on the density at the point where the functionalis evaluated (Kohn and Sham) .LDA, which in essence assumes that the density corresponds to that of a homogeneous electron gas, proved to be an improvement over HF. While LDA remains a major workhorse in solid state physics, its success in chemistry is at best moderate due to its strong tendency for over binding. The first real breakthrough came with the creation of functionals belonging to the so-called generalized gradient approximation (GGA) that incorporates dependence not only on the electron density but also on its gradient, thus being able to better describe the inhomogeneous nature of molecular densities. GGA functionals such as BP86 [3]) or PBE [20] can be implemented efficiently and yield good results, particularly for structural parameters, but are often less accurate for other properties. The next major step in the development of DFT was the introduction of hybrid functionals, which mix GGA with exact Hartree–Fock exchange [2]. Now days, hybrid DFT with the use of the B3LYP functional [3] is the dominant choice for the treatment of transition metal containing molecules.This method has shown good performance for a truly wide variety of chemical systems and properties. Transition metal complexes have achieved considerable interest in the field of physics, chemistry, and biology. These metal complexes show a wide variety of biological activity such as antitumoral [13, fungicidal [1] bactericidal, or antiviral [14].They have been used for metal analysis for device application relative to telecommunications optical computing, storage and information processing. Several investigators have studied EPR parameters of transition metal complexes [4, 15, 16, 17, 18, 19, 21 23, 25, 26, 27, 28,] and have obtained good agreement with the experimental results. In this work we have represented the first extensive evaluation of DFT methods for the prediction of hyperfine coupling constants for [Mn(CN)4] 2- , [Cr(CO)4] + ,and Co (CO)4] Isotropic transition metal complexes. Results obtained for these complexes using eight different density functionals eight density functional BLYP, BP86, BPW91, B3LYP, B3PW91, BHLYP, BHP86, BHPW91 have been compared with reliable experimental data.

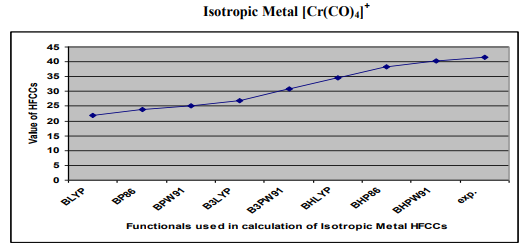
Figure1.0- Shows hyperfine coupling constant A values obtained from BLYP, BP86, BPW91, B3LYP, B3PW91, BHLYP ,BHP86, BHPW91, density functionals and experiment for Isotropic Metal Complex [Mn(CN)4N]-

Results - BHPW91> BHP86 > BHLYP > BLYP > BP86> BPW91> B3LYP > B3PW91 >EXP

Figure2.0- Shows hyperfine coupling constant A values obtained from BLYP, BP86, BPW91, B3LYP, B3PW91, BHLYP ,BHP86, BHPW91, density functionals and experiment for Isotropic Metal Complex [Cr(CO)4] +

Results - BLYP >BP86 >BPW91>B3LYP >B3PW91> BHLYP >BHP86 >BHPW91 >EXP

Figure3.0- Shows hyperfine coupling constant A values obtained from BLYP, BP86, BPW91, B3LYP, B3PW91, BHLYP ,BHP86, BHPW91, density functionals and experiment for Isotropic Metal Complex [Co (CO)4]

Results - BHPW91> BHP86> BHLYP> BLYP > BP86 > BPW91> B3PW91> B3LYP >EXP.

RESULTS
The results of the EPR parameter hyperfine coupling constant of different transition metal complexes considered for the DFT calculation in this work, obtained by the application of different density functionals BLYP, BP86 , BPW91, B3LYP , B3PW91 , BHLYP , BHP86 , BHPW91, and experiments are listed in Table No1.The hyperfine coupling constant values obtained from different DFT functionals of different complexes are also shown in Figure 1, 2,3.From the Figure 1, 2, 3, and Table 1, the results obtained by different density functional may be compared with experimental results. From the comparison of hyperfine coupling constants values obtained from different density functionals with experimentally observed values of the complexes considered in this study the performance of different functional have been found as follows. 1-Isotropic Metal Complex [Mn(CN)4N]- Results - BHPW91> BHP86 > BHLYP > BLYP > BP86> BPW91> B3LYP > B3PW91 >EXP. From these results it is inferred that result obtained by DFT functional B3PW91 is in close to the experimental result so the performance of this functional best for calculation EPR parameter hyperfine coupling constant A for Isotropic Metal Complex [Mn(CN)4N]- where as result obtained by BHPW91is very y poor and this functional is not appropriate for the calculation of EPR parameter hyperfine coupling constant A for this complex. 2-Isotropic Metal Complex [Cr(CO)4] + Results - BLYP >BP86 >BPW91>B3LYP >B3PW91> BHLYP >BHP86 >BHPW91 >EXP. In this case of Isotropic Metal Complex[Cr(CO)4] + , result obtained by DFT functional BHPW91 is in close to the experimental result so the performance of this functional best for calculation EPR parameter hyperfine coupling constant A for Isotropic Metal Complex Isotropic Metal Complex[Cr(CO)4] + where as result obtained by BLYP is very y poor and this functional is not appropriate for the calculation of EPR parameter hyperfine coupling constant A for this complex. 3-Isotropic Metal Complex [Co (CO)4] Results - BHPW91> BHP86> BHLYP> BLYP > BP86 > BPW91> B3PW91> B3LYP >EXP. In the case of Isotropic Metal Complex [Co (CO)4] , result obtained by DFT functional B3LYP is in close to the experimental result so the performance of this functional best for calculation EPR parameter hyperfine coupling constant A for Isotropic Metal Complex [Co (CO)4where as result obtained by BLYP is very y poor and this functional is not appropriate for the calculation of EPR parameter hyperfine coupling constant A for this complex. CONCLUSION From the above results it is inferred that that although the DFT calculated values of hyperfine coupling values obtained from different density functional for hyperfine coupling constant A have been found in close agreement with the experimental values but the better performance of the different functionals have been found different for different metal complexes .We have not identified any such functional, the results of which is excellent for all three metal complexes considered for study in this work. The performance of the DFT functional B3PW91 have been found better for Isotropic Metal Complex [Mn(CN)4N]- , B3LYP for Isotropic Isotropic Metal Complex [Co (CO)4] where as the DFT functional >BHPW91 is better for Isotropic Metal Complex [Cr(CO)4] + The theoretical results for hyperfine coupling constant obtained in this investigation suggesting that further development of density functionals is needed.

ACKNOWLEDGMENT
The authors acknowledge the immense help received from the research scholars and scientists whose articles are cited and included in references of this manuscript. The authors are also grateful to authors/editors/publishers of all those articles, journals and books from where the literature for this article has been reviewed and discussed. The authors would like to thank Dr .R.N Patel ,Prof.K.B.Ponday and Dr.H.Surya Prakash.Rao for valuable suggestions.

References:

1. Bermejo, E.R. Caballo, A. Castineiras, R. Dominguez, C. Maichle-Mossmer, J. Strahle and D.X. West Polyhedron: 18, 3695, 1999.

2. Becke AD J Chem Phys:98, 1372, 1993. 3. Becke AD Phys Rev A: ,38, 3098, 1988. 4. Christian Remenyi, Markéta L. Munzarová, and Martin KauppJ. Phys. Chem. B:109 (9), 4227, 2005.

5. Guest, M.F. in Lecture Notes in Chemistry, 44, Ed. M. Dupuis, Springer Verlag :98, 1986.

6. Hertwig, R. H. Holthausen, M. C. Koch, W. Z. B. Maksic Int. J. Quant. Chem: 54, 147,1995.

7. Hohenberg, P. W. Kohn, Phys. Rev:136, B864. 1964.

8. Hohenberg P, Kohn W Inhomogeneous electron gas. Phys Rev B :136,864,1964.

9. K awamoto. T.B.S. Hammes. R. Ostrander. A.L. Rheingold and A.S. Borovik Inorg. Chem: 32, 3424, 1998.

10. Kohn W, Sham LJ Phys Rev A: 140,1133, 1965b.

11. Kohn, P.W. Phy.Rev:136,1964.

12. Kohn W.and.Sham. L.J Phy.Rev:140,1965.

13. Kang.Y.N.Yang.S.O.kang.J.Ko.C.H.Lee and Y.H.Lee.Orgnometallics:16, 5522, 1997.

14. Kawamoto. T.B.S. Hammes. R.Ostrander. A.L. Rheingold and A.S. Borovik Inorg.Chem :32, 3424, 1998.

15. Kaupp. Martin ; R. Roman ; M. Olga A. Alexei ; S. Bernd ; M .Vladimir G. ; Inc. J Comput Chem :23,794, 2002.

16. Munzarova M, Kaupp M J Phys Chem A: 103, 9966. 1999.

17. Munzarova ML, Kubacek P, Kaupp M J Am Chem Soc: 122, 11900, 2000.

18. Markéta L. Munzarováand ,Martin KauppJ. Phys. Chem. B: 105 (50), 12644, 2001.

19. Neese F, Petrenko T, Ganyushin D, Olbrich G Coord Chem Rev: 251,288, 2007b.

20. Perdew JP, Burke K, Ernzerhof M PhysRevLett:77,3865, 1996.

21. Prajapati Vinita and Verma P.L.Acta Sciencia India :37, 3,295,2011

22. Schreckenbach, G. T. Ziegler, Theor. Chem. Acc.: 99 71, 1998.

23. Shamov, G. A. G. Schreckenbach, T. N. Vo Chem. Eur. J: 13, 4932, 2007.

24. Slater, J. C. Phys. Rev.: 81, 385. 1951. 25. Szabo A, Ostlund NS Modern quantum chemistry. McGraw-Hill, New: 1989.

26. Verma P.L. and Prajapati Vinita, Acta Sciencia India: 37,3, 287,2011.

27. West, D.K J.K.Swearingen,J.Valdesmartinez,S. Hernandez,Ortega,A.K.El-Sawaf V.Mours,A.castineiras,I.Gareciaand e.bermejo,Polyhedron:18,2919, 1999. 28. William M. Ames and Sarah C. Larsen J. Phys. Chem.A: 114 (1), 589, 2010.