IJCRR

IJCRR - 4(2), January, 2012

Pages: 06-12

Print Article   Download XML  Download PDF

ACCEPTANCE DECISION RULE OF REPETITIVE GROUP SAMPLING FOR BURR TYPE XII
DISTRIBUTION

Author: Muhammad Aslam

Category: General Sciences

Abstract:In this paper, acceptance decision rule of repetitive group sampling for Burr type XII distribution is given for known/unknown shape parameters. Two real lifetime examples from Lio et al. (2010) are selected to explain the procedure when the shape parameters of the Burr type XII distribution are unknown in practice. The two points approach on operating characteristics (OC) curve is used to construct the tables for industry use. Examples are given to illustrate the repetitive group sampling plans.

Keywords: Group acceptance sampling; repetitive sampling; life tests; producer‘s risk and consumer risks; Burr type XII distribution

Full Text:

1. INTRODUCTION
The reputation of companies depends upon the high reliability of their products. Now a day, different companies compete with each other on the basis of quality and reliability. Consumer prefers those items which is more reliable than others items. Inspection of the final product is very necessary to set the reliability or lifetime of the product. Even advanced machinery is available to produce high quality product. But, without proper inspection it is almost not possible to set the standard of the quality. For example, during the manufacturer of the US quartz (1/4 $), after strict inspection coins are sent to banks. In the lot, if few coins are not according to standard the complete lot of quartz is discarded. Inspection of the item is done on the basis of few items selected from the lot of the product. So, producer and consumer risks are always there. The researchers are trying to propose various types of acceptance sampling plans to minimize these risks. Producer and consumer are interesting to adopt that sampling plan which not only minimize their risks but also provides better protection of rejecting the good lots and accepting the bad lot respectively. In life testing experiment, single sampling is usually given more importance due to simplicity in application. In single acceptance sampling scheme, the acceptance number is fixed and sample of items are put on the test for some pre-fixed experiment time. If the number of defective items are larger than acceptance number, the lot is rejected, otherwise accepted. Single acceptance sampling is studied by many authors for several statistical distributions. Recently, single acceptance sampling was studied by Kantam et al. (2001), Rosaiah et al. (2006), Balakrishnan et al. (2007), Tsai and Wu (2006), Aslam and Kantam (2008), Aslam et al. (2010), Aslam et al. (2010) for Pareto distribution of 2nd kind, Lio et al. (2010a, 2010b) and Aslam et al. (2010). According to Aslam and Jun (2009 a, b) that the single sampling scheme is applicable when the experimenter has the facility to put single item on the single tester. Testers accommodating more than single item are available in practice. The number of items in a single tester in called the group and if sampling is done using the groups this is called the group acceptance sampling. For example, sudden death testing is always done in groups, for more detail see Jun et al. (2006). Aslam and Jun (2009 b) introduced the group sampling in time truncated experiment for log-logistic distribution and inverse Rayleigh distribution considering only consumer‘s risk. Aslam and Jun (2009 a) proposed the group plan for the Weibull distribution. According to Sherman (1965) the attribute repetitive group plan is more efficient than the single sampling plan even its operation is similar to sequential sampling. For more detail about attribute repetitive sampling reader may refer to Sherman (1965). Many authors including Balamurali and Jun (2006) provided the variable repetitive plans and compared the results with single plans. In the literature, study about the attribute sampling is available for the normal distribution. Burr type XII distribution attracted the attention of the researcher due its applications in many areas. This distribution is originally derived by Burr (1942) and is widely used in the area of quality control, reliability analysis and failure time models. More recently, Lio et al. (2010 a, b) produced excellent paper by introducing this distribution in area of acceptance sampling. They used two real data sets to fit the Burr type XII distribution and explained results with Further, no study is available for repetitive group plans for the Burr type XII distribution using the percentile life of the product. So, in this paper, we provided the repetitive group plans for the Burr type XII distribution. The rest of the paper is organized as: Design of proposed plan is given in Section 2. Advantage of the proposed plan is discussed in Section 3. Some examples are given in Section 4. In the last section, concluding remarks are given.

2. Design of the Proposed Plan Aslam and Jun (2009 a, b) originally proposed the group plan under the time truncated experiment in terms of mean ratio for Weibull distribution. We proposed the following repetitive group plan based on the original group plan. Step-1 Select the number of groups g and allocate predefined r items to each groups so that the sample size for a lot will be n=r g. Step-2 Accept the lot if the number of failures, D , is smaller than or equal to 1 c in every group. Truncate the test and reject the lot of the product as soon as the number of failures, D, from a group exceeds 2 c where 2 1 c c . Step-3 If the number of failures, D , with 1 2 c D c , for every group, then go to step and repeat the experiment. The proposed plan is characterized by three parameters which are 1 c , 2 c and g. The proposed repetitive group plan is generalization of many plans. The plan reduces to ordinary single plan when =1. Further, this plan reduces to Aslam and Jun (2009 a, b) plan if 1 2 c c The probability of acceptance and probability of rejection for this plan is given below respectively

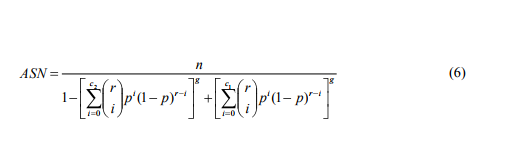
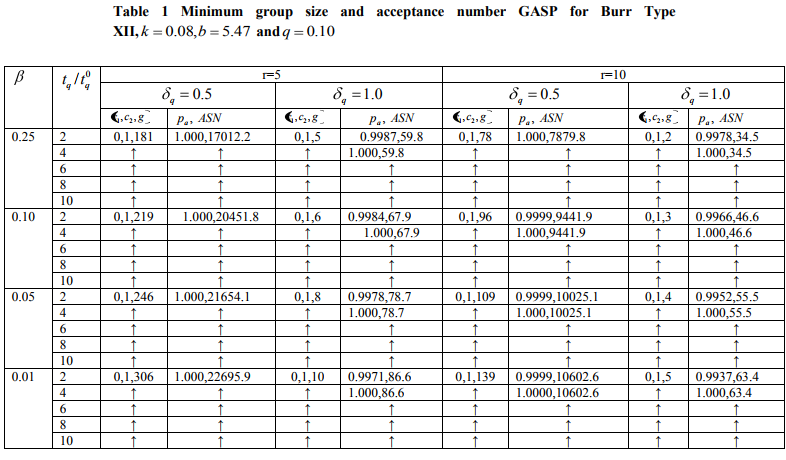
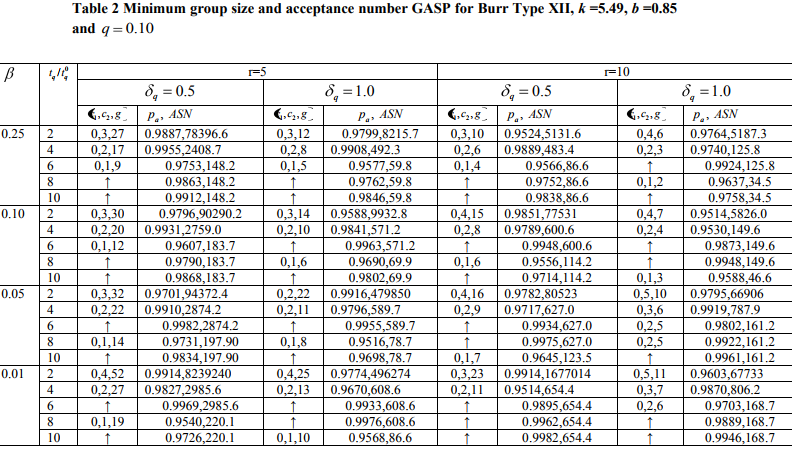
The design parameters of proposed plan are found using the simulation process such that the Eq. (4) and Eq. (5) should satisfy at minimum average sample number (ASN). While implementing the program for the proposed plan we noted that several combinations of plan parameters are available. As suggested Balamurali and Jun (2006), we selected that combination that provides the minimum ASN at consumer‘s risk. The plan parameters of this plan are determined for various values of =0.25, 0.10, 0.05, 0.01, q = 0.5, 1.0, 0 / q q t t 2, 4, 6, 8, 10, q =0.10, k =0.08, 5.49, r =5, 10 and b =5.47, 0.85. The plan parameters are placed in Table 1-2. From Table 1, we can observe that as 0 / q q t t increases from 2 to 10, the values of g remains same. But, as q increases from 0.5 to 1.0, we can see that g decreases. It is interesting to note that all the plan parameters are determined for 1 c =0 and 2 c =1. The ASNs for each plan is also given in Tables 1-2. As 0 / q q t t increases from 2 to 10, Table 1 shows that g remains the same; however, Table 2 shows that g decreases. From Tables 1-2, we can see that the repetition of the experiment is needed and g reduces when r increases from 5 to 10. Tables 1-2 are around here The similar tables for other values of shape parameters can be considered to find the suitable plan parameters combination. A program is available with author upon request. If shape parameter is unknown, it can be estimated from the previous data.

3. Comparison of Plans
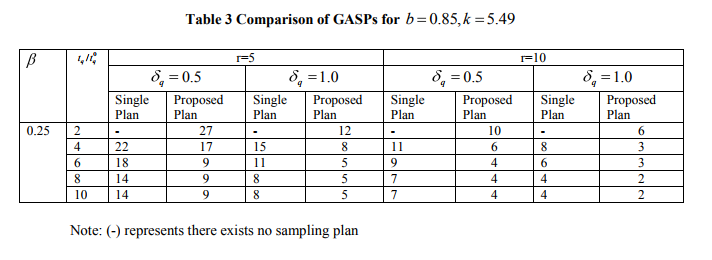
We compare the single group acceptance sampling plan with repetitive group sampling plan for b 0.85, k 5.49, =0.25, q 0.5 ,1.0 and =5, 10. The group sizes from both plans are placed in Table 3. From this table, we can see that for any percentile ratio the proposed plan provides the less group size (sample size). For example, for ratio=4, q 0.5 and =10, the sample size from the single sampling plan is 110 and from the proposed plan it is 60. For the proposed we need approximately 50% less sample size to reach the same decision about the submitted lot of the product. So, the proposed plan is more efficient that the single group acceptance plan. Table 3 is around here

4. Application
Example-1 Assume that the lifetime of a product have a Burr type XII distribution with k =5.49 and b =0.85. Suppose that an experimenter would like to use the proposed plan to establish the true unknown 10th percentile lifetime for the product is at least 6 months and experiment will be stopped after 6 months. This information leads to q =1.0. Further suppose that the in laboratory the experimenter has facility to install five items on a single tester. Let =0.05 when / 4 0 q q t t and =0.05 for this experiment. Then from Table 2 with r 5 , the plan parameters are ( 0, 2, 11) c1 c2 g . This plan is implemented as follows: select a random sample of 55 items and distribute into 11 groups. Accept the lot if no failure is recorded and reject it if more than 2 failures are recorded before 6 months. If the number of failures is greater than 0 and less than 3, then repeat the experiment. From Table 4, the probability of acceptance is 0.9796 and ASN=589.7for this plan.

5. CONCLUSION
Repetitive group acceptance sampling plan for the time truncated life tests is proposed when life time of the product follows the Burr type XII distribution. The plan is explained with the help of examples. The results of the proposed plan are compared with single group sampling plans and found that the proposed plan is more efficient than the single plan. It is suggested that to save time and cost of the life test experiments, the proposed plan should be applied in industry. Further, the proposed plan can be used to test/inspect many electronic components. The present study can be extended to some other distribution including alpha distribution, gamma distribution and generalized exponential distribution as future research.

ACKNOWLEDGEMENTS
The writer thanks the referees and editor for several valuable comments.

References:

1. Aslam, M. and Jun, C.-H. (2009a). A group acceptance sampling plan for truncated life test having Weibull distribution, Journal of Applied Statistics, 36(9), 1021-1027.

2. Aslam, M., Ahmad, M. and Razzaque, A. (2010). Group Acceptance Sampling Plan For Lifetimes Having Generalized Pareto Distribution, Pakistan Journal of Commerce and Social Sciences, 4 (2), 185-193.

3. Aslam, M., and Kantam, R.R.L. (2008). Economic acceptance sampling based on truncated life tests in the Birnbaum-Saunders distribution, Pakistan Journal of Statistics, 24(4), 269-276.

4. Aslam, M., Jun, C.-H, and Ahmad, M. (2009b). A group sampling plan based on truncated life tests for gamma distributed items. Pakistan Journal of Statistics. 25 (3), 333-340.

5. Aslam, M., Kundu, D. and Ahmad, M. (2010). Time truncated acceptance sampling plan for generalized exponential distribution, Journal of Applied Statistics (UK), 37(4), 555- 566.

6. Balakrishnan, N., Leiva, V. and Lopez, J. (2007). Acceptance sampling plans from truncated life tests based on the generalized Birnbaum-Saunders distribution. Communication in Statistics-Simulation and Computation, 36, pp. 643-656.

7. Balamurali, S. and Jun, C.-H. (2006), Repetitive group sampling procedure for variables inspection. Journal of Applied Statistics, 33(3), 327-338.

8. Burr, I.W. (1942). Cumulative frequency functions, Annals of Mathematical Statistics, 13, 215–232.

9. Jun, C.-H., Balamurali, S. and Lee, S.- H. (2006). Variables sampling plans for Weibull distributed lifetimes under sudden death testing. IEEE Transactions on Reliability, 55(1), pp. 53-58.

10. Kantam, R.R. L., Rosaiah, K. and Rao, G.S. (2001). Acceptance sampling based on life tests: Log-logistic models. Journal of Applied Statistics, 28(1), pp.121-128.

11. Lio, Y. L., Tsai, T.-R. and Wu, S.-J. (2010a). Acceptance sampling plans from truncated life tests based on the Birnbaum-Saunders distribution for percentiles, Communication in Statistics: Simulation and Computation, 39, 119-136.

12. Lio, Y. L., Tsai, T.-R. and Wu, S.-J. (2010b). Acceptance sampling plans from truncated life tests based on the Burr type XII percentiles, Journal of the Chinese Institute of Industrial Engineering, 27 (4), pp. 270-280.

13. Rosaiah, K., Kantam, R.R.L. and Santosh Kumar, Ch. (2006). Reliability of test plans for exponentiated loglogistic distribution, Economic Quality Control, 21(2), pp.165-175.

14. Sherman, R. E. (1965). Design and evaluation of repetitive group sampling plan, Technometrics, 7, pp. 11–21.

15. Tsai, T.-R. and Wu, S.-J. (2006). Acceptance sampling based on truncated life tests for generalized Rayleigh distribution. Journal of Applied Statistics, 33(6), pp. 595-600.