IJCRR

IJCRR - 4(6), March, 2012

Pages: 89-104

Print Article   Download XML  Download PDF

VIBRATIONAL SPECTRAL STUDIES, NLO AND NBO ANALYSES OF 2-CHLORO-4-NITROBENZOICACID
BASED ON DENSITY FUNCTIONAL THEORY

Author: V. Balachandran, A. Janaki, A. Lakshmi

Category: Technology

Abstract:In this work a combined theoretical and experimental study of 2-chloro-4-nitrobenzoic acid (CNBA) is reported using density functional theory (DFT) calculations as well as Raman and IR spectra have been recorded in the region 4000?400 cm?1 and 3500?100 cm?1, respectively. The optimized molecular geometry, normal mode wavenumbers, infrared intensities and Raman activities, corresponding vibrational assignments and intramolecular hydrogen bonds were investigated with the help of B3LYP method using 6-311G and cc-pVDZ basis sets. A detailed interpretation of the infrared and Raman spectra of CNBA is reported. The theoretical spectrograms for FT-IR and FT-Raman spectra of the title molecule have been constructed. The observed and calculated frequencies are found to be in good agreement stability of the molecule arising from hyper-conjugative interactions, leading to its bioactive charge delocalization have been analyzed using natural bond orbital (NBO) analysis

Keywords: 2-chloro-4-nitrobenzoic acid; Density functional theory; FT-IR; FT-Raman spectra; vibrational frequencies

Full Text:

INTRODUCTION
Recent spectroscopic studies of benzoic acid and its derivatives have been motivated by their biological and pharmaceutical importance. The aromatic acids are crystalline substances, generally slightly soluble in water and well soluble in polar organic solvents (alcohol, chloroform, benzene). Aromatic acids have all the properties characteristic of the carboxylic acids of the aromatic series. In medicine, aromatic acids are employed as weak antiseptics, and their salts as carriers of specifications [1]. Benzoic acid acts as a better inhibitor compared to salicylic acid with equal concentration [2]. The industrial applications are as a corrosion inhibitor, as an additive to nucleating agents for polyolefin, as a dye intermediate, as a stabilizer in photographic processing, and as a catalyst. Organic substances produced naturally in the higher plants, are used for controlling growth or other physiological functions. Benzoic acid is one of the most commonly used preservatives in cosmetics, foodstuffs, and drug preparations [3,4]. To the best of our knowledge, very few fields have been developed specifically for carboxylic acids. However, the lower acids like formic, and acetic acids have been extensively studied, and a few studies exist for the higher acids. Quantum chemical calculations involving carboxylic acids have to account for the electron-rich carboxyl group. Consideration of these factors motivated us to undertake the vibrational spectroscopic studies of the title compound for the electron rich carboxyl group. Consideration of these factors motivated us to undertake the vibrational spectroscopic studies of the title compound benzoic acid. The goal of present study is to give a complete description of the molecular geometry and molecular vibrations of the title compounds. The assignments of bands in the vibrational spectra of molecules are an essential step in the application of vibrational spectroscopy for solving various structural chemical problems.

EXPERIMENTAL DETAILS
The compound under investigation namely CNBA was obtained by Lancaster Chemical Company, UK, which is of spectroscopic grade, and hence used for recording the spectra as such without any further purification. The room temperature Fourier transform infrared spectrum of the title compound was measured in the region 4000–400 cm 1 at a resolution of ±1 cm 1 using a BRUKER IFS-66V FT-IR spectrometer equipped with KBr pellet was used in the spectral measurements. The FT-Raman spectrum of CNBA was recorded on a BRUKER IFS 66V model interferometer equipped with an FRA-106 FT-Raman accessory in the region 3500–100 cm 1 stokes region using the 1064 nm line of a Nd:YAG laser for excitation operating at 200 mW power. COMPUTATIONAL DETAILS The entire calculation was performed at B3LYP/6-311G and B3LYP/cc-pVDZ methods on personal computer using Gaussian 09W [5] program package, invoking gradient geometry optimization [6]. The optimized structural parameters were used in the vibrational frequency calculations at the B3LYP/6-311G and B3LYP/cc-pVDZ level to characterize all stationary points as minima. The natural bonding orbital (NBO) calculations were performed using NBO program as implemented in Gaussian 09W[5] package at B3LYP/cc-pVDZ level in order to understand various secondorder interactions between the filled and unfilled orbitals of the system, which is a measure of the intramolecular delocalization or hyperconjugation. By combining the results of the GAUSSVIEW program [7] along with symmetry considerations, vibrational frequency assignments were made with a high degree of accuracy. The Raman activities (Si) calculated by the Gaussian-09 program were converted to relative Raman intensities (Ii) using the following relationship derived from the basic theory of Raman scattering.

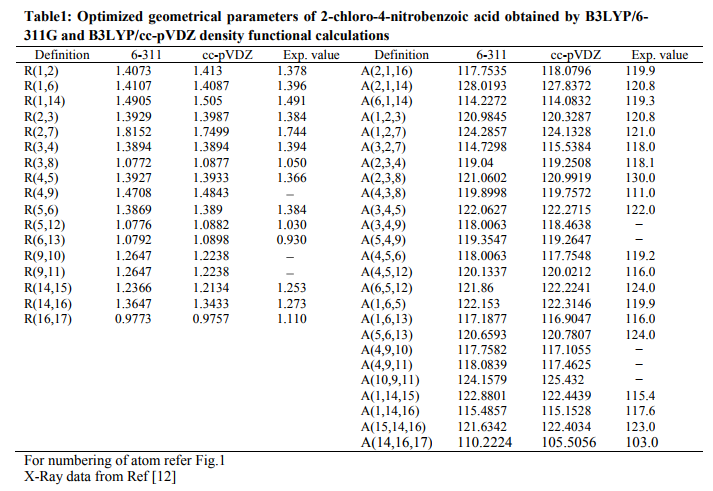
where 0 is the exciting frequency (in cm 1 units), i is the vibrational wave number of the ith normal mode, h, c, and k are universal constants, and f is the suitably chosen common normalization factor for all the peak intensities. The simulated FT-Raman and FT-IR spectra were plotted from the calculated intensity values using pure normal Lorentzian band shape with a band width of 10 cm 1 . The analysis for the vibrational modes of CNBA was presented in some detail in order to better describe the basis for the assignments. All the parameters were allowed to relax and all the calculations converged to an optimized geometry which corresponds to a true energy minimum, as revealed by the lack of imaginary values with wavenumber calculations. The Cartesian representation of the theoretical force constant has been computed at the fully optimized geometry by assuming the molecule belongs to Cs point group symmetry. The transformation force field from Cartesian to internal local symmetry coordinates, scaling the subsequent normal coordinate analysis (NCA), calculation of potential energy distribution (PED) were done on a PC with the version V7.0–G77 of the MOLVIB program written by Sundius [8, 9]. RESULTS AND DISCUSSION Molecular geometry The molecular structure along with numbering of atoms of CNBA is shown in Fig. 1. The maximum number of potentially active observable fundamentals of a non-linear molecule which contains N atoms is equal to (3N−6), apart from three translational and three rotational degrees of freedom [10]. Since the molecule do not possess any rotational, reflection or inversion symmetry. The most optimized structural parameters (bond length, bond angle) by B3LYP, with 6-311G and ccpVDZ basis sets were shown in Table 1. From the theoretical values, we can find that most of the optimized bond lengths are slightly larger than the experimental values, due to that the theoretical calculations have been carried out on isolated molecule in gaseous phase whereas the experimental results correspond to molecules in solid state. The optimized bond lengths of C−C in phenyl ring of similar molecule [11]. One can notice that the theoretical results as the experimental ones show that the lengths of C3−C4 and C5−C6 bonds are shorter than the other bonds of the ring, leading to a pseudoquinoidal character of the benzene ring. The optimized C−N bond lengths are 1.4708Å for B3LYP/6-311G method and 1.4843Å for B3LYP/cc-pVDZ method, which are also in agreement with those of values reported in the literature [12]. For the C−O bonds, the calculated lengths (Table 1) are slightly shorter than in 2-aminobenzoic acid (1.320Å) [13]. It is interesting to note that both N14−O15 and N14−O16 bond lengths in nitro group is same, that is 1.2647 Å whereas in 2- nitropyridine both the N−O bond lengths are different. This effect can be attributed to the repulsion between the loan electron pair on the N ring nitrogen atom.

Vibrational assignments
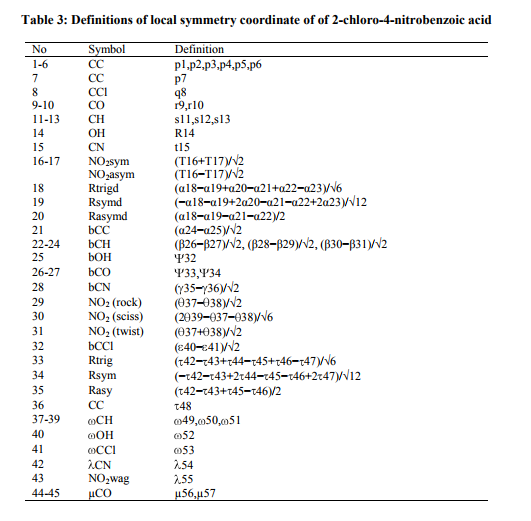
A detailed description of vibrational modes can be given by means of normal coordinate analysis. For this purpose, the full set of 57 standard internal coordinates containing 12 redundancies were defined as given in Table 2. From these, a non-redundant set of local symmetry coordinates were constructed by suitable linear combinations of internal following the recommendation by Rauhut and pulay et al .[14] and they are presented in Table 3. The theoretically calculated DFT force fields were transformed to this later set of vibrational coordinares and used in all subsequent calculation. The experimental FT-IR and FT- Raman spectra are shown in Fig 2 and 4, respectively.

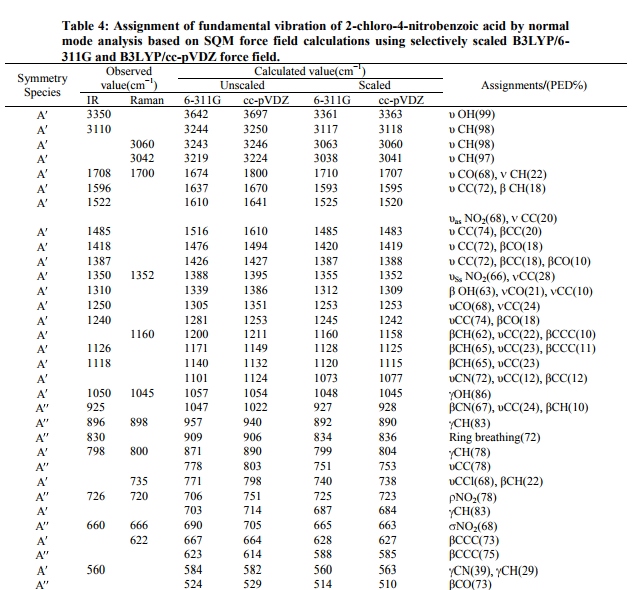
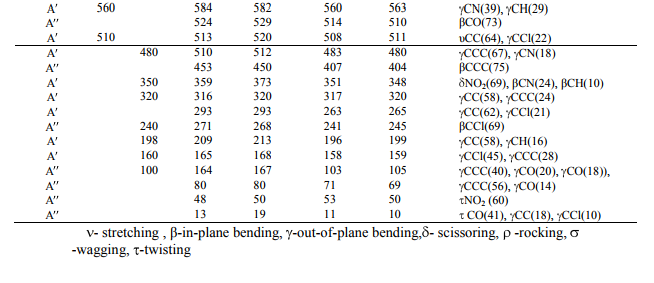
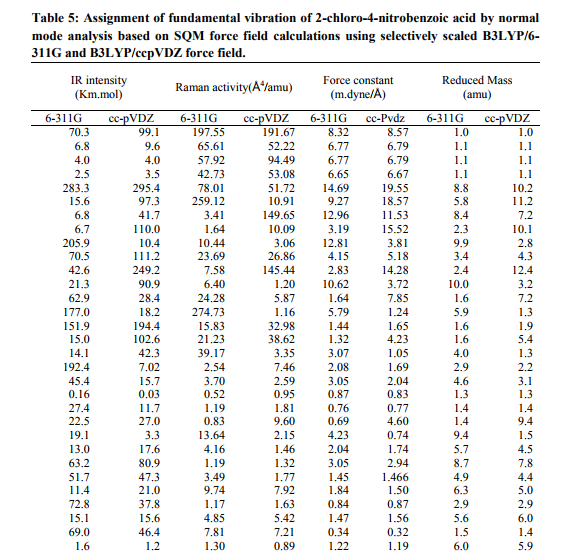
The observed and calculated wavenumbers and normal mode descriptions for the title compound are reported in Table 4. When using computational methods to predict normal vibrations for relatively complex polyatomic molecules, scaling strategies are used to bring computed wavenumbers. The vibrational frequencies obtained from B3LYP were suitably scaled using the various scale factors for stretching, in-plane bending, out-of-plane bending, and ring vibrations. The vibrational assignments in the present work are based on the B3LYP frequencies, infrared intensities, Raman activities as well as characteristic group frequencies. In agreement with Cs symmetry, all the 45 vibrations are distributed as 17 stretching vibrations, 15 inplane and 13 out-of-plane vibrations of same symmetry species. Assignments were made through visualization of the atomic displacement representations for each vibration, viewed through GAUSSVIEW [7] and matching the predicted normal wavenumbers and intensities with experimental data. It is convenient to discuss the vibrational spectra of CNBA in terms of characteristic spectral regions as described below. C−H vibrations Since CNBA is a trisubstituted heterocyclic aromatic system, it has only one C−H moiety. The hetero aromatic structure shows the presence of C−H stretching vibrations in the region 3100−3000 cm−1 which is the characteristic region for the ready identification of C−H stretching vibrations [15]. The expected C−H stretching vibrations correspond to the scaled vibration stretching modes of C4−H unit. The vibrations assigned by Gauss view program package at 3117, 3063, 3038, and 3118, 3060, 3041 cm 1 by B3LYP/6-311G and B3LYP/ccpVDZ levels respectively, show good agreement with weak FT-IR band at 3110 cm 1 and 3060, 3042 in FT-Raman band. In general in-plane and out-of-plane aromatic C−H deformation vibrations occur in the region 1300−1000 and 600−1000 cm 1 , respectively. The C−H in–plane bending vibration computed at 1160, 1128, 1120 cm 1 by B3LYP/6-311G method shows good agreement with FT-IR band at 1126, 1118 and 1160 cm 1 in FT-Raman band. The C−H out-ofplane bending vibration appears at 896 and 798 cm 1 in FT-IR and in FT-Raman at 898 cm 1 shows good agreement with computed B3LYP method. In general the C−H vibrations (stretching, in-plane and out-of-plane bending) computed by both the methods show good agreement with experimental observation as well as literature data. C–C vibrations The C−C aromatic stretching, known as semicircle stretching vibration predict at 1593/1595 cm 1 by B3LYP method show deviation from the experimental observation in FT-IR band at 1596 about 1 cm 1 . The C−C aromatic stretch, known as semicircle stretching, predicted B3LYP/6-311G at 1485 cm 1 is in excellent agreement with experimental observations of 1485 cm 1 in FT-IR band. The calculated values for the ring breathing mode is coincide satisfactorily with medium strong FTIR band at 830 cm 1 [16] The theoretically calculated C−C−C out-of-plane bending and inplane bending modes have been found to be consistent with the recorded spectral value and they are shown in Table 4. COOH vibrations O−H stretching band is characterized by very broad band appearing near about 3400 cm 1 . The band observed at 3350 cm 1 has its origin in the O−H stretching vibration. However the calculated wave number shows positive deviation of 11/13 cm 1 may due to the presence of hydrogen bonding. The C=O stretching is a characteristic frequency of carboxylic acid. The band appearing at 1708/1700 cm 1 is assigned as C=O stretching vibration in FT-IR/FT-Raman spectra. The theoretically computed value of 1710/1707 cm 1 shows very good agreement with experimental results. OH in-plane bending occurs between 1440 and 1395 cm 1 and out-ofplane bending occurs between 960 and 875 cm 1 . A band at 1310 cm 1 in FT-IR is assigned as OH in-plane bending vibration and frequency at 1050 cm 1 is assigned as OH out-of-plane bending vibration. However the calculated value of OH out-of-plane bending deviates negatively by about 233 cm 1 may be due to fact that OH out-of-plane bending deformation mode. The present assignments agree well with values available in the literature [17−21]. C−COOH vibrations In CNBA, the band at 1240 cm 1 in FT-IR spectrum corresponds to C−COOH stretching vibrations. However the calculated results do support this. The bands at 263/265 cm 1 is computed to C−COOH in-plane and 196/199 cm 1 out-of-plane bending by B3LYP method. The computed value of above said vibrations coincides exactly at 198 cm 1 . The above results are in good agreement with earlier work [22]. The force constant values computed at B3LYP level of theories at cc-pVDZ and 6-311G basis sets have been shown in Table 5. These force constant values on comparison with related molecules are found to deviate approximately by one unit. NO2 vibrations The asymmetric and symmetric stretching vibrations of NO2 generally give rise to bands in the regions 1500−1570 and 1300−1370 cm 1 in nitro benzene and substituted nitro benzenes [23], respectively. In accordance with above conclusion the band at 1522 cm 1 in FT-IR corresponds to NO2 symmetric stretching vibrations. The theoretically scaled values at 1525 and 1520 cm 1 by B3LYP method exactly correlates with experimental observations. The deformation vibrations of NO2 group (rocking, wagging and twisting) contribute to several normal modes in the low frequency region [24, 25]. It follows from Table 4, the band observed at 726 cm 1 in FT-IR and 720 cm 1 in FT-Raman spectra correspond to NO2 rocking vibration of the title molecule. It should be emphasized that the wave number calculated by B3LYP/6-311G method for the NO2 rocking mode at 725 cm 1 is in very good agreement with the corresponding experimental data. The NO2 wagging vibration contributes mainly to the normal mode, which is observed as a band at 660 cm 1 in FT-IR spectrum and 666 cm 1 in FT-Raman spectrum. The theoretically calculated value by B3LYP/6- 311G method at 665 cm 1 shows an excellent agreement with experimental data. It should be emphasized that the wave number calculated by B3LYP method at 53/50 for NO2 torsion mode is in agreement with the assignment proposed by Kanna Rao and Syam Sundar [26]. However, this type of vibrations is not supported by experimental data. C Cl vibrations The vibrations belonging to the bond between the ring and the halogen atoms are worth to discuss here, since mixing of vibrations are possible due to the lowering of the molecular symmetry and the presence of heavy atoms on the periphery of molecule [27]. The assignments of C Cl stretching and deformation vibrations have been made by comparison with similar molecules, the halogen substituted benzene derivatives [28]. Mooney [29] assigned vibrations of C X group (X=Cl, Br and I) in the frequency range of 1129 480 cm 1 . The strong FT-Raman band at 735 cm 1 corresponds to C Cl stretching mode. The theoretical wave number of C Cl 738 cm 1 coincides very well with the scaled value. The C Cl in-plane and out-of-plane bending vibration are assigned to the FT-IR bands at 240, and 160 cm-1 , respectively. Computed IR intensity and Raman activity analysis Computed vibrational spectral IR intensities and Raman activities of the corresponding wave numbers by B3LYP/6-311G and B3LYP/ccpVDZ basis set have been collected in the Table 5. Comparison of the IR intensities and Raman activities calculated by B3LYP/6-311G and B3LYP/cc-pVDZ levels with experimental values exposes the variation of IR intensities and Raman activities. These variations may due to the substitution of the chlorine, acid and nitro group atoms.

Vibrational force constant
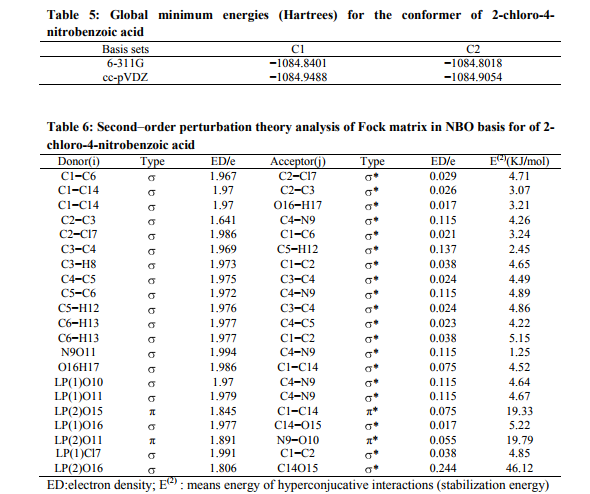
The output files of the quantum mechanical calculations contain the force constant matrix in Cartesian coordinates and in Hartree/ Bohr2 units. These force constants were transformed to the force fields in the internal local-symmetry coordinates. The force field determined was used to calculate the vibrational potential energy distribution among the normal coordinate. In this molecule the values show the variation due to the substitution of the chlorine, acid and nitro groups. They are listed in Table.5. NBO analysis Natural bonds orbital analysis picture of CNBA because all orbital are mathematically chosen to include the highest possible percentage of the electron density. Interaction between both filled and virtual orbital spaces information correctly explained by the NBO analysis, it could enhance the analysis of intra- and inter-molecular interactions. The second-order Fock matrix was carried out to evaluate donor (i) – acceptor (j) i.e. donor level bonds to acceptor level bonds interaction in the NBO analysis [30]. The result of interaction is a loss of occupancy from the the concentration of electron NBO of the idealized Lewis structure into an empty non-Lewis orbital. For each donor (i) and acceptor (j), the stabilization enrgy E(2) associates with the delocalization i to j is estimated as j i i j ij i F E E q 2 (2) ( , ) ) where qi is the donor orbital orbital occupancy, are i and j diagonal elements and F(i, j) is the off diagonal NBO Fock matrix element. Natural bond orbital analysis provides a convenient basis for investigating charge transfer or conjugative interaction in molecular systems. Some electron donor orbital, acceptor orbital and the interacting stabilization energy resulted from the secondorder micro-disturbance theory are reported [31, 32]. The larger E(2) value the more intensive is the interaction between electron donors and acceptor i.e. the more donation tendency from electron donors to electron acceptor and the greater the extent of conjugation of the whole system [33]. Delocalization of electron density between occupied Lewis type (bond or lone pair) NBO orbital and formally unoccupied (anti bond or Rydgberg) non-Lewis NBO orbital correspond to a stabilizing donor-acceptor interaction. NBO analysis has been performed on the CNBA molecule at the ccpVDZ level in order to elucidate, the intra-molecular rehybridization and delocalization of electron density within the molecule. The intra molecular interaction is formed by the orbital overlap between (C1−C14) and * (C2−C3) bond orbital, which results intramolecular charge transfer causing stabilization of the system. The electron density of O16−H17 is 1.97e. The most important interactions in the CNBA molecule having lone pair O11 (2) with that of anti bonding N9−O10, results the stabilization of 19.79 KJ/mol. The interaction between lone pair O16 with anti-bonding C14−O15 resulting stabilization energy 46.12 KJ/mol, which denotes larger delocalization, is shown in Table 6.

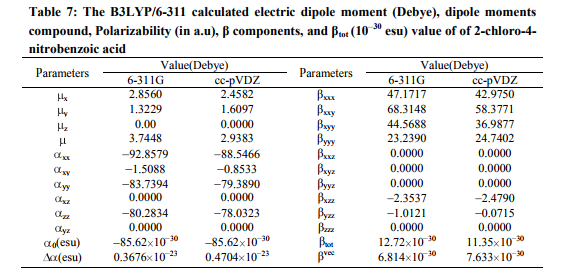
Prediction of first hyperpolarizability a NLO property There is an intense current research activity in the area of molecular activity in linear and nonlinear optics, devoted to the search for efficient, stable, simple organic molecules exhibiting large hyperpolarizabilities [34 37]. Even though several promising structural motifs have been identified, aromatic backbone molecules are still common and show large non-linear optical properties. Organic non-linear materials have attracted a keen interest in recent years owing to their potential applications in various photonic technologies. Significant effects have focused on studying the electronic and structural properties of donor acceptor substituted π-conjugated organic molecules with large molecular nonlinear optical (NLO) response (β, first-order hyperpolarizability). Two factors are attributed to NLO properties of such molecules in an electric field: the altered ground state charge distribution by the donor and acceptor moieties and the enhanced –π-electronic charge redistribution through the π -conjugation. The experimental spectroscopic behavior described above is well accounted for by ab initio calculations in π-conjugated systems that predict exceptionally large Raman and infrared intensities for the same normal modes. It is also observed in our title compound that the bands at 1350, 1050, 896,798, 726 and 660 cm 1 in FT-IR spectrum have their counterparts in Raman 1352, 1045, 898, 800, 720, and 666 cm−1, which shows that the relative intensities in IR and Raman spectra are comparable. The first hyperpolarizability β is associated with the intramolecular charge transfer (ICT), resulting from the electron cloud movement through the π-conjugated framework from electron donor to electron acceptor groups. A reliable prediction of molecular hyperpolarizability requires adequate basis sets and therefore must involve both diffuse and polarization functions. As the basis becomes larger, one expects a better description of the molecule and, accordingly, more accurate results. In the view of these points, B3LYP/6- 311G method has been used for present study in order to see the effects of the level of theory and basis sets. The title is molecule fully optimized at B3LYP/6-311G method in the Gaussian 09 program. The tensor components of the static first hyperpolarizabilities β, and, βvec- , are calculated for the title molecule by taking into account the Kleinman symmetry relations and the squared norm of the Cartesian expression for the β tensor. The relevant expressions used for the calculation are shown below: The total static dipole moment is 

The total static dipole moment, polarizabilities and first hyperpolarizabilities of CNBA were calculated. Table 7 lists the values of the electric dipole moments (Debye) and dipole moment components, polarizabilities and hyperpolarizabilities of the CNBA. Analyzing the β and β vec, it can be seen that there is the additive contribution of off-diagonal β-vectors to the total due to substitution in benzene. Such kind of behavior (large off diagonal contributions) has high practical utility in the research on NLO materials [38]. The total dipole moment (µ) and mean polarizability are 3.7448, 2.9383 Debye and 85.62 10 30esu, 85.62 10 30respectively. The µ×β value shows that there is significant increase in optical nonlinearities of the title molecule.

Mulliken population analysis:
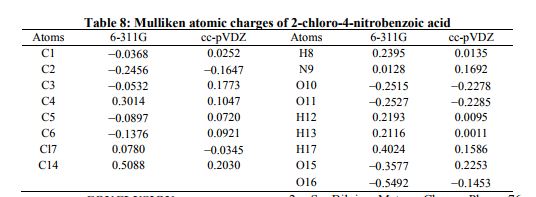
Mulliken Atomic Charges Mulliken atomic charge calculation [39] has an important role in the application of quantum chemical calculation to molecular system. Because the atomic charges affect dipole moment, polarizability, electronic structure and more a lot of properties of molecular systems. The total atomic charges of CNBA were obtained by Mulliken population analysis with 6-311G basis set are listed in Table.8. For the title compounds the Mulliken atomic charge of C14 and H17 atoms occupies the higher positive value and becomes high acidic. Their corresponding Mulliken atomic charges of CNBA are 0.508843 and 0.402492, respectively. For CNBA molecule the O15 and O16 atoms have negative value. This clearly indicates the presence of intra molecular weak hydrogen bonding (C?O…H).

CONCLUSION
In the present work, we have performed the experimental and theoretical vibrational and HOMO, LUMO analysis of CNBA for the first time. The equilibrium geometry computed by B3LYP/cc-pVDZ level for both the bond lengths and bond angles are performed better. The vibrational frequencies analysis by B3LYP method agrees satisfactorily with experimental results. On the basis of agreement between the calculated and experimental results, assignments of all the fundamental vibrational modes of CNBA were examined and proposed in this investigation. Therefore, the assignments made at higher level of theory with higher basis set with only reasonable deviations from the experimental values, seem to be correct. NBO results reflect the transfer mainly due to N9−O10 and C14−O15. This study demonstrates that scaled B3LYP calculations are powerful approach for understanding the vibrational spectra of medium sized organic compounds. Finally, the calculated HOMO−LUMO energies show that charge transfer occur within the molecule which is responsible for bioactive and NLO properties of the molecule. For CNBA molecule the O15 and O16 atoms have negative value. This clearly indicates the presence of intra molecular weak hydrogen bonding (C?O…H).

References:

1. G. Melentyeva, L. Antonova, Pharmaceutical Chemistry, Mir Publishers: Moscow (1988) 223.

2. S. Bilgic, Mater. Chem. Phys. 76 (2002) 52 58.

3. D.P. Gowing, W. Leeper, Bot. Gaz. 121 (1960), 249 267.

4. D. Cynthia, B.A. Downard, L. Jackson Roberts II, D.Jason Morrow, Clinical Pharmacology and therapeutics. Division of Clinical Pharmacology, Departments of Medicine and Pharmacology, Vanderbilt University School of medicine: Nashville, Tenn, 1994.

5. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 2009, Revision A.02 Gaussian, Inc., Wallingford CT, 2009.

6. H.B. Schlege, J. Comput. Chem. 3(1982) 214 218.

7. A. Frisch, A.B. Nielsen, A.J. Holder, Gaussview Users Manual, Gaussian Inc., Pittsburg, 2000. 8. T. Sundius, Journal of Molecular Strucutre 218(1990) 321 326.

9. (a) T. Sundius, Vibrational Spectroscopy 29(2009) 89 95, (b) Molvib,V.7.0: Calculation of Harmonic Force Fields and Vibrational modes of molecules, QCPE Program No.807(2002).

10. M. Silverstein, G. Clayton Basseler, C. Morill, Spectrometric Identification of Organic Compounds, Wiley, NewYork, 1981.

11. M. Kurt, M. Trudakul, S. Yurdakul, J. Mol. Struct. (Theochem.) 711(2004) 25 32.

12. V. Krishnakumar, R. John Xavier, Spectrochim. Acta A 61(2005) 253 260.

13. H.Takazawa, S. Ohba, Y. Saito, Acta Crystallogr 42 (1986) 1880 1881.

14. G. Rauhut, P. Pulay, J. Phys. Chem 99(1995) 3039 3100.

15. M. Silverstein, G. Clayton Basseler, C. Morill, Spectrometric Identification of Organic Compounds, Wiley, New York, 1981.

16. N.P. Sing, R.A. Yadav, Ind. J. Phys. B 75 (4) (2001) 347 355.

17. P. Venkoji, Ind. J. Pure Appl. Phys. 24 (1986) 166 172.

18. J. Marshal, Ind. J. Phys. 72B (1998) 661 667.

19. S. Thakur, V.P. Gupta, Ind. J. Pure Appl. Phys. 36 (1998) 567.

20. T. Syed, P.K. Verma, Ind. J. Phys. 57B (1983) 413.

21. M. Chaman, P.K. Verma, Ind. J. Phys. 77B (3) (2003) 315 318.

22. S. Ahmad, S. Mathew, P.K. Verma, Ind. J. Pure Appl. Phys. 30 (1992) 764.

23. E.F. Mooney, Spectrochim. Acta 20 (1964) 1021 1032.

24. J.H.S. Green, D.J. Harrison, Spectrochim. Acta 26A (1970) 1925.

25. J.H.S. Green, H.A. Lauwers, Spectrochim. Acta 27A (1971) 817.

26. R.A. Kanna Rao, N. Syam Sundar, Spectrochim. Acta 49A (1993) 1691.

27. R.A. Yadav, I.S. Sing, Ind. J. Pure Appl. Phys. 23 (1985) 626 627.

28. G. Varsanyi, Assignments For vibrational Spectra of Seven Hundred Benzene Derivatives, Vols. 1 2, Adam Hilger, 1974.

29. E.F. Mooney, Spectrochim, Acta 20 (1964) 1021.

30. C. James, A. Amal Raj, R. Rehunathan, I. Hubert Joe, V.S. Jayakumar, J. Raman Spectrosc. 379 (2006) 1381. 31. J.N. Liu, Z.R. Chen, S.F. Yuan, J. Zhejiang Univ.Sci. 6B (2005) 584 589.

32. S. Sebastain, N. Sundaraganesan, Spectrochim. Acta A 75 (2010) 941 952.

33. S.J.A. Van Gisbergen,J.G. Sniiders and E.J. Baserends, Phy Rev Lett 78,1997.

34. U.Gubler, S. Concilio, C. Bosshard, I. Biaggio, P. Gunter, R.E. Martin, M.J. Edelmann, J. Wytko and F. Diederich. Appl. Phy Lett 81(2002),2322 2324.

35. P. Acebad,S. Blaya and L. Carretero, J . Phy B:At Mol Opt Phy. 36(2003), 2445 2454.

36. G. Maroulis, ed., Atoms, Molecules and Clusters in Electric field, Imperial College Press, London, 2006.

37. J.L. Bredas, C. Adant, P. Tackx, A. Persoons and B.M. Pierce, Chem. Rev. 94(1994), 242.

38. J.J. Wolf, F. Siegler, R. Matschiner, R. Wortmann, Angew. Chem. Int. Ed. Eng.39 (2000). 39. D.R. Kanis, M.A. Ratner, T. Marks, J. Chem. Rev. 94(1994) , 195 and references cited therein.