IJCRR

IJCRR - 4(13), July, 2012

Pages: 06-15

Date of Publication: 18-Jul-2012

A CHARACTERIZATION OF OSCILLATORY MOTIONS FOR ROTATORY CONVECTION IN COUPLE-STRESS FLUID

Author: Ajaib S. Banyal

Category: General Sciences

Abstract:The rotatory-thermal instability of a couple-stress fluid heated from below is investigated. Following the
linearized perturbation stability theory and normal mode analysis, the paper mathematically established
the condition for the onset of oscillatory motions which may be neutral or unstable for rigid boundaries at
the top and bottom of the fluid. It is established that all non-decaying slow motions starting from rest, in
a couple-stress fluid of infinite horizontal extension and finite vertical depth, which is acted upon by uniform vertical rotation opposite to gravity and a constant vertical adverse temperature gradient, are necessarily oscillatory, if 4 8 2 1 F TA , where A T is the Taylor number and F is the couple-stress parameter, the result is also in accordance with corresponding configuration of Newtonian fluid when the couple-stress parameter F=0, by Gupta etal 1 .

Keywords: Thermal convection; Couple-Stress Fluid; Rotation; PES; Taylor number.

Full Text:

INTRODUCTION
In the subject matter like hydrodynamic stability where experiments has led to the theory all along, the main source of arriving at a mathematical breakthrough is to have a feeling for the right result that may have been suggested from nowhere or through the application of intuitive reasoning based on experience and observation. Right from the conceptualizations of turbulence, instability of fluid flows is being regarded at its root. The thermal instability of a fluid layer with maintained adverse temperature gradient by heating the underside plays an important role in Geophysics, interiors of the Earth, Oceanography and Atmospheric Physics etc. A detailed account of the theoretical and experimental study of the onset of Bénard Convection in Newtonian fluids, under varying assumptions of hydrodynamics and hydromagnetics, has been given by Chandrasekhar 2 . The use of Boussinesq approximation has been made throughout, which states that the density changes are disregarded in all other terms in the equation of motion except the external force term. Sharma et al 3 has considered the effect of suspended particles on the onset of Bénard convection in hydromagnetics. The fluid has been considered to be Newtonian in all above studies. Scanlon and Segel 4 have considered the effect of suspended particles on the onset of Bénard convection and found that the critical Rayleigh number was reduced solely because the heat capacity of the pure fluid was supplemented by that of the particles. With the growing importance of non-Newtonian fluids in modern technology and industries, the investigations on such fluids are desirable. Stokes 5 proposed and postulated the theory of couple-stress fluid. One of the applications of couple-stress fluid is its use to the study of the mechanism of lubrication of synovial joints, which has become the object of scientific research. A human joint is a dynamically loaded bearing which has articular cartilage as the bearing and synovial fluid as lubricant. When fluid film is generated, squeeze film action is capable of providing considerable protection to the cartilage surface. The shoulder, knee, hip and ankle joints are the loaded-bearing synovial joints of human body and these joints have low-friction coefficient and negligible wear. Normal synovial fluid is clear or yellowish and is a viscous, non-Newtonian fluid. According to the theory of Stokes 5 , couple-stresses are found to appear in noticeable magnitude in fluids very large molecules. Since the long chain hylauronic acid molecules are found as additives in synovial fluid. Walicki and Walicka 6 modeled synovial fluid as couplestress fluid in human joints. Sharma and Thakur 7 have studied the thermal convection in couple-stress fluid in porous medium in hydromagnetics. Sharma and Sharma 8 have studied the couple-stress fluid heated from below in porous medium. The use of magnetic field is being made for the clinical purposes in detection and cure of certain diseases with the help of magnetic field devices. Sharma et al. 9 have studied the effect of suspended particles on couple-stress fluid heated from below and found that suspended particles have stabilizing effect on the system. Sharma and Sharma 10 have studied the effect of suspended particles on couple-stress fluid heated from below in the presence of rotation and magnetic field and found that rotation has a stabilizing effect while dust particles have a destabilizing effect on the system. Sunil et al. 11 have studied the effect of suspended particles on couple-stress fluid heated and soluted from below in porous medium and found that suspended particles have stabilizing effect on the system. Thermosolutal convection in a couple-stress fluid in the presence of magnetic field and rotation, separately, has been investigated by Kumar and Singh 12 &13 . Kumar and Kumar 14 have studied the combined effect of dust particles, magnetic field and rotation on couple-stress fluid heated from below and for the case of stationary convection, found that dust particles have destabilizing effect on the system, where as the rotation is found to have stabilizing effect on the system, however couple-stress and magnetic field are found to have both stabilizing and destabilizing effects under certain conditions. Sunil et al. 15 have studied the global stability for thermal convection in a couple-stress fluid heated from below and found couple-stress fluids are thermally more stable than the ordinary viscous fluids. Pellow and Southwell 16 proved the validity of PES for for the classical Rayleigh-Bénard convection problem. Banerjee et al 17 gave a new scheme for combining the governing equations of thermohaline convection, which is shown to lead to the bounds for the complex growth rate of the arbitrary oscillatory perturbations, neutral or unstable for all combinations of dynamically rigid or free

boundaries and, Banerjee and Banerjee 18 established a criterion on characterization of nonoscillatory motions in hydrodynamics which was further extended by Gupta et al. 1 . However no such result existed for non-Newtonian fluid configurations, in general and for couple-stress fluid configurations, in particular. Banyal 19 have characterized the non-oscillatory motions in couple-stress fluid in the presence of suspended particles. Keeping in mind the importance of nonNewtonian fluids, the present paper is an attempt to characterize the onset of instability analytically, in a layer of incompressible couple-stress fluid heated from below in the presence of uniform vertical rotation opposite to force field of gravity, when the bounding surfaces of infinite horizontal extension, at the top and bottom of the fluid are rigid. It is shown that for the configuration under consideration that, if 1 4 8 2 F TA , then an arbitrary neutral or unstable modes of the system are definitely nonoscillatory and, in particular the PES is valid, where TA is the Taylor number.

FORMULATION OF THE PROBLEM AND PERTURBATION EQUATIONS
Considered an infinite, horizontal, incompressible couple-stress fluid layer, of thickness d, heated from below so that, the temperature and density at the bottom surface z = 0 are T0 , 0 respectively and at the upper surface z = d are Td , d and that a uniform adverse temperature gradient dz dT is maintained. The fluid is acted upon by a uniform vertical rotation 0,0, . Let , p, T and q u,v,w denote respectively the density, pressure, temperature and velocity of the fluid. Then the momentum balance, mass balance equations of the couple-stress fluid (Stokes 1 (1966), Chandrasekhar 1 (1981) and Scanlon and Segel 1 (1973)) are

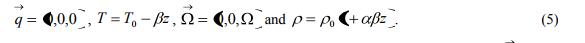
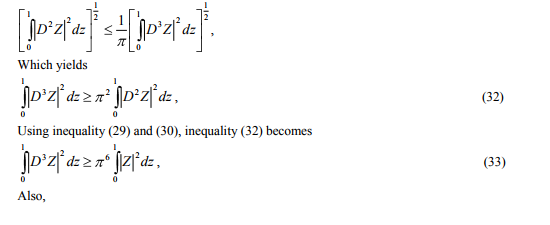
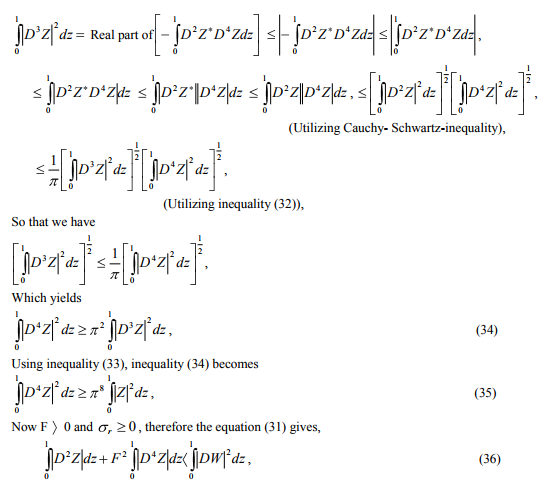
RESULTS
Presented otherwise from the point of view of existence of instability as stationary convection, the above theorem can be put in the form as follow:- Theorem 2: The sufficient condition for the validity of the ?exchange principle‘ and the onset of instability as a non-oscillatory motions of nongrowing amplitude in a couple-stress fluid, heated from below, in the presence of uniform vertical rotation is that, 1 4 8 2 F TA , where TA is the Taylor number and F is the couple-stress parameter, when the boundaries are rigid. or The onset of instability in a couple-stress fluid, heated from below, in the presence of uniform vertical rotation, cannot manifest itself as oscillatory motions of growing amplitude if the Taylor number TA and the couple-stress parameter F, satisfy the inequality 1 4 8 2 F TA , when both the bounding surfaces are rigid. In the context of existence of instability in ?oscillatory modes‘ and that of ?overstability‘ in the present configuration, we can state the above theorem as follow:- Theorem 3: The necessary condition for the existence of instability in ?oscillatory modes‘ and that of ?overstability‘ in a couple-stress fluid heated from below, in the presence of uniform vertical rotation is that the Taylor number TA and the couple-stress parameter of the fluid F, must satisfy the inequality 1 4 8 2 F TA , when both the bounding surfaces are rigid

DISCUSSIONS AND CONCLUSIONS
This theorem mathematically established that the onset of instability in a couple-stress fluid in the presence of uniform vertical rotation, cannot manifest itself as oscillatory motions of growing amplitude if the Taylor number TA and the couple-stress parameter of the fluid, satisfy the inequality 1 4 8 2 F TA , when both the bounding surfaces are rigid. The essential content of the theorem, from the point of view of linear stability theory is that for the configuration of couple-stress fluid of infinite horizontal extension heated form below, having rigid boundaries at the top and bottom of the fluid, in the presence of uniform vertical rotation, parallel to the force field of gravity, an arbitrary neutral or unstable modes of the system are definitely non-oscillatory in character if 1 4 8 2 F TA , and in particular PES is valid and it improved the domain of the result of Banyal and Singh 22 . Further, the result is also in accordance with corresponding configuration of Newtonian fluid when the couple-stress parameter F=0, by Gupta et al 1 .

ACKNOWLEDGEMENT
Author acknowledges the immense help received from the scholars whose articles are cited and included in references of this manuscript. The authors are also grateful to authors / editors /publishers of all those articles, journals and books from where the literature for this article has been reviewed and discussed. The author is highly thankful to the referees for their very constructive, valuable suggestions and useful technical comments, which led to a significant improvement of the paper.

References:

1. Gupta, J.R., Sood, S.K., and Bhardwaj, U.D., (1986), On the characterization of nonoscillatory motions in rotatory hydromagnetic thermohaline convection, Indian J. pure appl.Math.,17(1) pp 100-107.

2. Chandrasekhar, S., (1981), Hydrodynamic and Hydromagnetic Stability, Dover Publication,

3. Sharma, R.C., Prakash, K. and Dube, S.N. (1976).Effect of suspended particles on the onset of Bénard convection in hydromagnetics, J. Math. Anal. Appl., USA, Vol. 60 pp. 227-35.

4. Scanlon, J.W. and Segel, L.A., (1973), Some effects of suspended particles on the onset of Bénard convection, Phys. Fluids. Vol. 16, pp. 1573-78

5. Stokes, V.K., (1966), Couple-stress in fluids, Phys. Fluids, Vol. 9, pp. 1709-15.

6. Walicki, E. and Walicka, A., (1999), Inertial effect in the squeeze film of couple-stress fluids in biological bearings, Int. J. Appl. Mech. Engg., Vol. 4, pp. 363-73

7. Sharma, R.C. and Thakur, K. D., (2000), Couple stress-fluids heated from below in hydromagnetics, Czech. J. Phys., Vol. 50, pp. 753-58

8. Sharma, R.C. and Sharma S., (2001), On couple-stress fluid heated from below in porous medium, Indian J. Phys, Vol. 75B, pp.59-61.

9. Sharma, R.C., Sunil, Sharma, Y. D. and Chandel, R.S,. (2002), On couple-stress fluid permeated with suspended particles heated from below, Archives of Mechanics, 54(4) pp. 287-298.

10. Sharma, R.C. and Sharma, M., (2004), Effect of suspended particles on couple-stress fluid heated from below in the presence of rotation and magnetic field, Indian J. pure. Appl. Math., Vol. 35(8), pp. 973-989

11. Sunil, Sharma, R.C. and Chandel, R.S., (2004), Effect of suspended particles on couple-stress fluid heated and soluted from below in porous medium, J. of Porous Media, Vol. 7, No.1 pp. 9-18

12. Kumar, P. and Singh, M. (2008), Magneto thermosolutal convection in a couple-stress fluid, Ganita Sandesh (india), Vol.21(2).

13. Singh, M. and. Kumar, P., (2009), Rotatory thermosolutal convection in a couple-stress fluid, Z. Naturforsch, 64a, 7(2009)

14. Kumar, V. and Kumar, S. (2011), On a couplestress fluid heated from below in hydromagnetics, Appl. Appl. Math., Vol. 05(10),pp. 1529-1542

15. Sunil, Devi, R. and Mahajan, A. (2011), Global stability for thermal convection in a couple stress- fluid, Int. comm.. Heat and Mass Transfer, 38,pp. 938-942

16. Pellow, A., and Southwell, R.V., (1940), On the maintained convective motion in a fluid from below. Proc. Roy. Soc. London A, 176, 312-43.

17. Banerjee, M.B., Katoch, D.C., Dube,G.S. and Banerjee, K. (1981). Bounds for growth rate of perturbation in thermohaline convection. Proc. R. Soc. A378, 301-04

18. Banerjee, M. B., and Banerjee, B. (1984), A characterization of nonoscillatory motions in magnetohydronamics. Ind. J. Pure & Appl Maths., 15(4), 377-382

19. Banyal, A.S., (2011) A characterization of nonoscillatory motions in couple-stress fluid in the presence of suspended particles (2011), J. Comp. and Math. Scis.(JCMS), Vol.2( 3), pp. 537-545.

20. Schultz, M.H. (1973). Spline Analysis, Prentice Hall, Englewood Cliffs, New Jersy

21. Banerjee, M.B., Gupta, J.R. and Prakash, J. (1992), On thermohaline convection of Veronis type, J. Math. Anal. Appl., Vol.179, No. 2 pp. 327-334.

22. Banyal, A. S. and Singh, K., (2011) A Characterization of Rotatory Convection in Couple-Stress Fluid, Int. J. of Fluids Engg., Vol. 3, No. 4, pp. 459-468.