IJCRR

IJCRR - 4(14), July, 2012

Pages: 69-78

Date of Publication: 31-Jul-2012

NUCLEATION KINETICS, XRD AND SHG STUDIES OF LALANINE SINGLE CRYSTALS GROWN AT DIFFERENT SUPERSATURATION LEVELS

Author: K.K.Hema Durga, P. Selvarajan, D.Shanthi

Category: General Sciences

Abstract:L-alanine crystal is a Nonlinear Optical (NLO) active amino acid and it is useful for the future photonic technology. Solubility and nucleation temperature were measured for L-alanine at different saturation temperatures and the sample of this work has positive temperature coefficient of solubility. Metastable zonewidth was obtained from the difference between the saturation and nucleation temperatures and it is
observed to be large at higher temperatures. Induction period measurements for the selected supersaturation levels at different temperatures were carried out for supersaturated aqueous solutions of
L-alanine and it is noticed that induction period decreases with supersaturation ratios. The critical nucleation parameters were evaluated based on the classical theory of homogeneous nucleation. The bulk crystals of L-alanine have been grown from the optimized growth parameters and at different supersaturation levels. Single crystal XRD studies and SHG measurement were carried out for L-alanine
samples grown at different supersaturation levels.

Keywords: Amino acid; L-alanine; nucleation kinetics; induction period; supersaturation; Gibbs free energy; growth from solutions; XRD; metastable zonewidth; SHG

Full Text:

INTRODUCTION
Amino acids are the repeating building blocks of molecular structure of the important compounds known as proteins and they are a group of organic compounds containing two functional groups such as amino and carboxyl groups. The key elements of an amino acid are carbon, hydrogen, oxygen and nitrogen. Although the neutrally charged structure for an amino acid is commonly written, it is inaccurate because the acidic COOH and basic NH2 groups react with one another to form an internal salt called a zwitterion. It has no net charge because of one positive (NH3 + ) and one negative charge (COO) [1-3] . L-alanine is an organic α-amino acid with the chemical formula CH3CHNH2COOH. It is a white odorless crystal powder and easily dissolves in water, slightly dissolves in alcohol and undissolves in ether. L-alanine is a conditionally essential amino acid and it is an important source of energy for muscle tissue, the brain and central nervous system. L-alanine strengthens the immune system by producing antibodies, helps in the metabolism of organic acids and sugars and is used by protein synthesis and immune system regulation [4,5]. It was first crystallized by Bernal [6] and later by Simpson [7] and Destro et al [8] and it is the simplest acentric crystal with second harmonic generation efficiency of about 0.3 times that of the well known KDP [9-12]. Considering the importance of L-alanine crystal, a research programme is being carried out in our laboratory to study the various physical and chemical properties of L-alanine and its complexes. Considerable interest has been stressed on this material because it is an NLO active material and is a technologically important material. In this work, an attempt has been made to determine the critical nucleation parameters, solubility, induction period, metastbale zonewidth of the recrystallized sample of L-alanine. Growth of bulk single crystals of L-alanine was carried out using the optimized growth parameters obtained from nucleation kinetic studies and grown crystals were subjected to single crystal XRD and SHG studies.

Theory for nucleation process
Nucleation is the precursor and the most important phenomenon for crystal growth. When few atoms, ions or molecules join together in a supersaturated solution, a cluster or nucleus is formed and the overall excess free energy ( G ) between the nucleus and solute in the supersaturated solution is given by G= Gs+ Gv (i) where Gs is the surface excess free energy and Gv is the volume excess free energy. Once the nucleation occurs in the supersaturated solution, the nucleus grows quickly and a bright sparkling particle is seen. The time of observation of the sparkling particle in the undisturbed solution from the time at which the solution reaches experimental temperature is called the induction period ( ). For a given volume of solution, the frequency of formation of nuclei is inversely proportional to the induction period. The expression for the induction period in terms of Gibbs free energy is given by ln = -B+ G/kT (ii) where B is a constant, k is the Boltzmann‘s constant, T is the absolute temperature. Usually nucleus formed in supersaturated solution is assumed to be spherical in shape. According to Gibbs theory in terms of surface thermodynamics, the overall excess free energy between a spherical nucleus and solute can be written as [13] G=4 r 2 +(4/3) r 3 Gv‘ (iii) where Gv‘ is the free energy change per unit volume, r is the radius of the nucleus and is the interfacial tension or surface energy per unit area. This energy will be maximum for certain value of r, which is known as critical radius. Nuclei formed with radius greater than this r are stable and decrease their free energy by growing [14,15]. According to Thomson-Gibbs equation, the volume excess free energy is given by Gv‘ = (kT/v)lnS (iv) where S is the supersaturation ratio and v is volume of a molecule. S is given by S = C/Co where C is the supersaturated concentration and Co is the saturated concentration. The net free energy change ( G) increases with the increase in size of nucleus, attains maximum and decreases with further increase in the size of nucleus. The size corresponding to the maximum free energy change is called critical nucleus . The radius of the critical nucleus can be obtained by setting the differentiation condition 

d ( G) / dr = 0
Differentiating equation (iii) we get,
d ( G) / dr = 8 r + 4 r 2 Gv‘ = 0
The size of critical nucleus is obtained by putting r = r* ,

r*= -2 / Gv‘ (v)
Substituting equation. (iv) in the equation (v), we get
r* = -2 v / kT ln S

Since N k = R and taking modulus r*= 2 vN/RTlnS (vi) Where R is the universal gas constant and N is the Avogadro‘s number. Substituting equation (vi) in the equation (iii), we get Gibbs free energy change for the critical nucleus (Here r = r* and G = G* for critical nucleus) G*= (16 3 v 2N 2 )/[3R2T 2 (lnS)2 ] (vii) Therefore, equation (ii) can be written for critical nucleus as ln = -B + (16 3 v 2 N 3 ) /[3R3 T 3 (ln S)2 ] (viii) A plot of 1/ (ln S)2 against ln from equation (viii) is straight line and the slope is m = (16 3 v 2 N 3 )/(3R3 T 3 ) (ix) Therefore, G* = mRT / [N (ln S)2 ] or G* = mkT /(ln S)2 (x) From equation (9) we have, = (RT/ N) [3m / (16 v 2 )]1/3 (xi) The number of molecules in a critical nucleus is found using the following equation n = (4/3) ( /v) r* 3 (xii) The nucleation parameters such as radius of the critical nucleus, Gibbs free energy change, interfacial tension and the number of molecules in the critical nucleus can be determined using the equations (vi), (x) , (xi) and (xii).

RESULTS AND DISCUSSION
Solubility and metastable zonewidth The Analytical Reagent (AR) grade salt of Lalanine was purchased commercially from Merck India and it was further purified by recrystallization. The solubility and metastable zonewidth for the re-crystallized salt of L-alanine were found at different saturation temperatures. Solubility study was carried out using a hot-plate magnetic stirrer and a constant temperature bath. A voltage regulator was attached with hot-plate magnetic stirrer in order to maintain the temperature constant. Initially, the temperature was maintained at 30 oC. The re-crystallized salt of L-alanine was added step by step to 50 ml of de-ionized water in an air-tight container kept on the hot-plate magnetic stirrer and stirring was continued till a small precipitate was formed. This gave confirmation of supersaturated condition of the solution. Then, 25 ml of the solution was pipetted out and taken in a petri dish and it was warmed up at 40 oC till the solvent was evaporated out. By measuring the amount of salt present in the petri dish, the solubility (in g/100 ml) of L-alanine in de-ionized water was determined and this method of measuring solubility is known as gravimetrical method [16]. The same procedure was followed to find solubility of L-alanine samples at various temperatures using a constant temperature bath. Metastable zonewidth is an essential parameter for the growth of good crystals from solution, since it is the direct measure of the stability of the solution in its supersaturated region. The difference between the saturated temperature and the nucleation temperature is taken to be the metastable zone width of a system. In the present work, metastable zonewidth for L-alanine sample saturated at different temperatures was determined by polythermal method [17]. In polythermal method, the equilibrium-saturated solution was cooled from the overheated temperature until the first visible crystal is observed. Since the time taken for the formation of the first visible crystal after the attainment of critical nucleus is very small, the first crystal observed may be taken as the critical nucleus. Using the solubility data, the saturated solution of L-alanine was prepared at 30 oC, and the solution was filtered into a beaker using Whatmann filter paper. This beaker was loaded into a constant temperature bath controlled to an accuracy of ±0.01 oC, provided with a cryostat for cooling below room temperature. The temperature of the solution was raised by 5 oC above the saturated temperature and the solution was continuously stirred for 3 hours using an immersible Teflon coated magnetic stirrer to ensure homogeneous concentration. Now the solution was cooled at the rate of 5 oC/h from this preheated temperature to a temperature at which the first speck of the nucleation appeared. Thus the temperature at which the first speck of nucleus in the saturated solution is noted and it is called the nucleation temperature. The experiment was repeated for solutions saturated at other temperatures like 35 and 40 oC. The plots of solubility curve and nucleation curve for the sample of this work at different saturation temperatures and at different concentrations are presented in figure 1. From the results, it is observed that the solubility increases with temperature and hence the sample of this work has positive temperature coefficient of solubility. The difference between saturation temperature and the nucleation temperature at a particular temperature gives the metastable zonewidth.

Measurement of induction period For the measurement of induction period, isothermal method [18] was used at the selected supersaturation ratios or levels viz. 1.1, 1.15, 1.2 and 1.25 saturated at temperatures such as 30, 35 and 40 oC. Using the solubility diagram, the recrystallized salt of L-alanine was used to prepare supersaturated aqueous solution (by keeping the supersaturation ratio at 1.1 initially ) in a corning glass beaker (nucleation cell), preheated slightly and it was stirred continuously for about 2 hours using a magnetic stirrer to ensure the homogeneous concentration. The nucleation cell was loaded into a constant temperature bath (controlled to an accuracy of 0.01 0C) and illuminated using a powerful lamp to observe the formation of nucleus. The temperature of the constant temperature bath was set at 30 oC and as the temperature reached the experimental temperature (30 oC ), the time was noted. When the first speck of nucleation occurred in the solution, again the time was noted. The time difference between the time of observation of the first speck particle in the nucleation cell and the time at which the solution reached the experimental temperature (30 oC) was the induction period ( ). Similarly, induction period measurements were performed at the other supersaturation ratios (S) and at other temperatures such as 35 and 40 oC. Two or three trials were carried out to ascertain the correctness of the results. From the results (Fig.1), it is noticed that the induction period decreases with the supersaturation ratio (S) and it is reduced when the solution of L-alanine is saturated at higher temperatures.

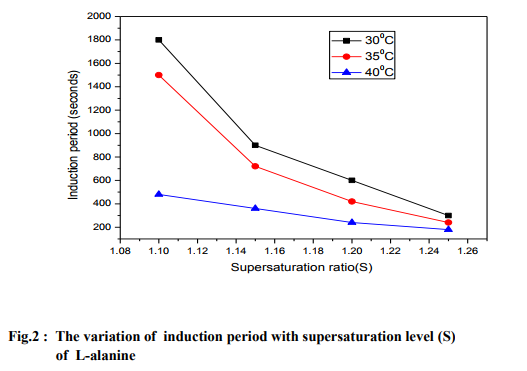
Determination of critical nucleation parameters
From the measured values of induction period, the critical nucleation parameters were determined. 2 were drawn for different temperatures such as 30, 35 and 40 oC and are presented in the figure 3. In the obtained results, it is noticed that the plots of ln against 1/(ln S)2 are approximately linear (slightly nonlinear) and this explains the classical theory of homogeneous nucleation. This is similar to the results observed by many researchers [19-21]. The effect of heterogeneous nucleation due to dust particles from air and scratchings on the inner walls of nucleation cell was reduced by carrying out the experiment in a relatively dust-free space and by using scratch-free glass beakers. The nonlinearity of plots may be due to heterogeneous nucleation caused by the impurities present in the solution. Using the values of slope, the nucleation parameters such as radius of the critical nucleus, Gibbs free energy change, interfacial tension and the number of molecules in the critical nucleus can be determined based on classical theory of homogeneous nucleation assuming the shape of critical nucleus as spherical. using the equations (vi), (x) , (xi) and (xii) and the obtained values are provided in the table 1.

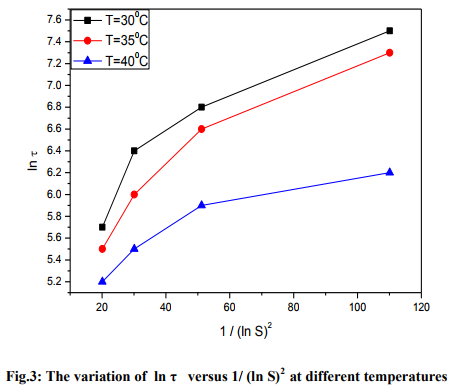
From the results, it is observed that induction (S) increases for the solutions supersaturated at 30, 35 and 40 oC. Studies on nucleation kinetics of L-alanine s are carried out in order to have the controlled nucleation rate. Nucleation and crystal growth kinetics in connection with the amount of material available for crystal growth determine the number and volume of crystals produced. The number of crystals produced in the supersaturated solution is expressed as nucleation rate i.e. the number of crystals produced per unit volume per unit time. The nucleation rate J were calculated using the equation J = A exp[- G* / (kT)] ( xiii) where A is the pre-exponential factor ( approximately A= 1 x 1030 for solution), G* is the critical free energy of the nucleus, k is the Boltzmann constant and T is the constant temperature of the solution [13] and are given in the table 1. It is noticed from the results that the values of G* , n, r* decrease with increase in supersaturation ratio (S). When G* increases, the nucleation rate decreases according to the above equation (xiii).

Based on the data obtained from the nucleation kinetic studies, the following optimized conditions are useful for the bulk growth of L-alanine single crystals: (i) Formation of multinuclei could be avoided when we use low supersaturation at higher saturation temperatures, (ii) metastable zonewidth is high and hence this leads to high stability of the solution at higher temperatures, (iii) Interfacial tension is low for the aqueous solution of L-alanine and hence water could be used to grow bulk crystals. The studies on induction period, metastable zonewidth, interfacial tension, nucleation rate and other nucleation parameters give ideas for the controlled growth of L-alanine crystals by slow evaporation and slow cooling methods. Growth of crystals at different saturation levels The optimized growth parameters from the studies of nucleation kinetics were used to grow good quality bulk single crystals. It took about 20 to 25 days to harvest the crystals. When the obtained data from nucleation kinetic studies are analyzed, the nucleation rate is low for solution of L-alanine supersaturated at 40 oC and hence spontaneous nucleation will be reduced if the crystals are grown using the solution of L-alanine supersaturated at 40 oC. In this work, L-alanine single crystals were grown by slow evaporation at different supersaturation levels viz. 1.1, 1.15, 1.2 , 1.25 supersaturated at 40 oC . Let these samples be coded as LA1, LA2,LA3, LA4. The grown crystals of this work are displayed in figures 4, 5, 6 and 7. It is observed that the morphology of Lalanine crystals has been changed when the supersaturation levels are altered.

Single crystal XRD studies
The grown crystals of this work (LA1, LA2, LA3 and LA4) were subjected to single crystal XRD studies using an ENRAF NONIUS CAD4 diffractometer with MoKα radiation (λ=0.71073A o ) and the obtained data for all the four samples are found to be same. The unit cell parameters obtained in this work are a = 6.034(2) Å, b = 12.331(4) Å, c o , V = 429.44(2) Å3 . The space group obtained for all the samples of different morphology is P212121 and this is a noncentrosymmetric crystal group which an essential condition for Second Harmonic Generation (SHG) in L-alanine material. The obtained XRD data for L-alanine crystal are found to be in good agreement with the data reported in the literature [22].

Measurement of SHG
The second harmonic generation (SHG) behavior of the powdered form of all the four samples of this work l was tested using the Kurtz and Perry method [23]. A high intensity Nd:YAG laser (λ=1064 nm) with a pulse duration of 6 ns was passed through the powdered sample. The green light was detected by a photomultiplier tube (PMT) and displayed on a Cathode Ray Oscilloscope(CRO). KDP crystal was powdered into identical size as that of the sample and it was used as reference material in the SHG measurement. The SHG was confirmed from the output of the laser beam having the green emission (λ=532 nm). The SHG efficiency of all the grown samples (LA1, LA2, LA3, LA4) are observed to be almost same and it is 0.322 times that of KDP crystal.

CONCLUSIONS
Solubility of L-alanine crystals was measured for various temperatures in the range 30-50 oC and it is observed that it increases with temperature. Metastable zonewidth was measured by finding nucleation temperature for the aqueous solution of L-alanine saturated at different temperatures. Classical theory of nucleation kinetic process was detailed and induction period was measured for Lalanine sample and it decreases with the supersaturation level and this leads to increase in the rate of nucleation of the crystals. Critical nucleation parameters such as interfacial tension, radius of critical nucleus, Gibbs free energy change and number of molecules in the critical nucleus were calculated. Growth of bulk single crystals of L-alanine was performed by solution method and it is observed that there is a change of morphology of crystals when supersaturation level of the solution is altered. Single crystal XRD study reveals the orthorhombic structure of the grown crystals. The measured SHG efficiency of the grown samples was found to be 0.322 times that of KDP crystal.

ACKNOWLEDGEMENT
The authors are grateful to Department of Science and Technology (DST ) and University Grants Commission (UGC) , Government of India for the financial support to carry out this work. Also the authors are thankful to the management of Aditanar College of Arts and Science, Tiruchendur for the encouragement given to us to carry out the research work.

References:

1. J.J. Rodrigues Jr, N.M. Barbosa Neto, D.T. Balogh, S.C. Zilio, L. Misoguti, C.R. Mendonc, Optics Communications 216 (2003) 233.

2. A.S.J. Lucia Rose, P. Selvarajan, S. Perumal, Mater. Chem. Phys. 130 (2011) 950.

3. L.Misoguti , A.T. Varela , F.D.Nunes,V.S. Bagnato ,F.F.A. Melo, J. Mendes Filho, S.C. Zilio ,Opt. Mater. 6 (1996) 147.

4. L. Brennan, A. Shine, C. Hewage, J. Paul, G. Malthouse, K.M. Brindle, N. McClenaghan, P.R. Flatt, P. Nemsholmer, Diabetes 51 (2002) 1714.

5. G.A. Cunningham, N.H. McClenaghan, P.R. Flatt, P. Newsholme, Clinical Sci. 109 (2005) 447.

6. J.D. Bernal, Z. Kristallogr 78 (1931) 363.

7. H.J. Simpson Jr., R.E. Marsh, Acta Cryst. 8 (1966) 550.

8. R. Destro, R.E. Marsh, R. Bianchi, J.Phys.Chem. 92 (1988) 966.

9. V. Bisder-Leib, M.F. Doherty, Cryst. Growth Des. 3 (2003) 221.

10. C. Razetti, M. Ardoino, L. Zanotti, M. Zha, C. Paorici, Cryst. Res. Technol. 37 (2002) 456.

11. A.S.J. Lucia Rose, P. Selvarajan, S. Perumal, Spectrochimica Acta Part A 81 (2011) 270.

12. Thenneti Raghavalu, G. Ramesh Kumar, S. Gokul Raj, V.Mathivanan, R.Mohan, J. Crystal Growth 307 (2007) 112.

13. A.E.Nielsen, S. Sarig, J. Cryst. Growth 8 ,1(1971) 1.

14. S. Boomadevi, R. Dhanasekaran, P. Ramasamy, Cryst. Res.Technol, 37 (2002) 159.

15. P.Santhanaraghavan, P. Ramasamy, Crystal Growth-Processes and Methods, KRU Publications, Kumbakonam, Tamil Nadu , India ( 2003).

16. P.Selvarajan, J.Glorium Arulraj , S.Perumal, J. Crystal Growth 311 (2009) 3835.

17. N.P. Zaitseva, L.N. Rashkovich, S.V. Bagatyatrva, J. Crystal Growth, 148 (1995) 276.

18. D.Jayalakshmi, J.Kumar, J. Crystal Growth, 292 (2006),528.

19. C.Mahadevan, G.Janiland Angel, V.Anton Sophana and V.Umayorubhagan, Bull. Mater. Sci. 22(1999)817.

20. Chen Jianzhong, Lin Sukun, Yang Fengtu, Wang Jiahe, Lang Jianming, J.Crystal Growth 179(1997)226.

21. K.V.Rajendran, R.Rajasekaran, D.Jayaraman, R.Jayavel, P.Ramasamy, Mat.Chem. Phys., 81(2003)50.

22. M. Lydia Carolinea,R. Sankar, R.M. Indirani, S. Vasudevan Mater. Chem.Phys. 114 (2009) 490.

23. S.K.Kurtz, T.T. Perry, J.Appl.Phys. 19 (1968) 3798.