IJCRR

IJCRR - 4(23), December, 2012

Pages: 152-161

Date of Publication: 15-Dec-2012

INFLUENCE OF IRREGULARITY AND INITIAL STRESS ON LOVE WAVES IN INHOMOGENEOUS ANISOTROPIC POROUS LAYER

Author: Rajneesh Kakar, Shikha Kakar

Category: Technology

Abstract:The influence of irregularity, initial stress and porosity on the propagation of Love waves in an inhomogeneous crustal layer over an inhomogeneous half space has been discussed. The irregularity has been taken in the half-space in the form of a parabola. It is observed that Love waves propagate in this assumed medium. The dispersion equation of phase velocity has been derived. It has been found that the phase velocity of Love waves is considerably influenced by porosity and anisotropy of the porous layer, inhomogeneity of the half-space and prestressing present in the media, the layer and the half-space. The effect of the medium characteristics on the propagation of Love waves has been analyised and results of numerical calculations have been presented graphically.

Keywords: Irregularity, Love Waves, Anisotropic, Initial Stress

Full Text:

INTRODUCTION
The study of wave propagation in elastic medium with different irregularities is of great importance to seismologists as well as to geophysicists to understand and pre- dict the seismic behavior at the different margins of earth. The earth has a layered structure, and this exerts a significant influence on the propagation of elastic waves. The simplest cases of influence exerted on the propagation of seismic waves by a single plane boundary which separates two half-spaces with different properties, and by two parallel plane boundaries forming a layer. Earth is being treated as an elastic body in which three types of waves can occur. 1. Dilatational and equivoluminal waves in the interior of the earth. 2. In the neighbourhood of its surface known as Rayleigh waves [1] 3. Third type of waves occur near the surface of contact of two layers of the earth known as Love waves [2] The Rayleigh waves are observed far from the disturbance source near the surface. Since the energy carried by these waves is concentrated over the surface, its dissipation is slower than the dilatational and equivoluminal waves where, the energy is dissipated over the volume of the disturbed region. Therefore, during earth quakes for an observer remote from the source of disturbance, the Rayleigh waves represent the greatest danger. In the case of Love waves, the energy is concentrated near the interface; hence they are dissipated more slowly. In the problem of propagation of Love type seismic waves in inhomogeneous isotropic media of finite depth lying over a infinite half space, it is shown that the distortional wave velocity in the layer is greater than that in the semi infinite half space. The basic literature on the propagation of elastic waves is the monograph written by Ewing et al.[3]. Vrettos [4] and Kennett and Tkal?cic′[5] gave much information on the effect of heterogeneity in the study of surface waves vibration due to line-load. The propagation of Love waves in an in homogeneous layer is of considerable importance in earth quakes engineering and seismology on account of occurrence of inhomogeneities in the crust of the earth as the earth is supposed to be made up of different layers. This problem has been studied by Anderson [6], Biot [7], Scholte [8], and Sinha [9] by considering different models of a layer changing either density or rigidity and established the presence of Love waves in each case. Chattopadhyay et al. [10] employed Ghosh method to study Love waves excited by a source in a layer overlying inhomogeneous half-space. Sinah [11] also considered this problem for variable rigidity in the layer by reducing it to a Bessel’s equation. The analysis, however, in this case becomes a little complicated. Also Gogna [12], Chadwick [13], Zhang [14] also studied the propagation of Love waves through nonhomogeneous media. By the virtue of Biot’s theory, many researchers studied surface waves Love and Rayleigh types, in an inhomogeneous media. Dey and Mahto Dey et al. [15] studied the effect of presence of rigid boundary on the propagation of Love waves in a sandwiched medium. The naturally occurring medium is often porous and liquid filled. The size of pores is assumed to be small and, macroscopically speaking, their average distribution is uniform. The role of pore-water in seismology has been emphasized in many studies. The diffusion of water and readjustment of fluid pressure has been in vague as a triggering mechanism for earthquakes. The present paper discusses the possibility of existence of Love wavse in an initially stressed anisotropic poro-elastic layer over a semi-infinite heterogeneous half space with linearly varying rigidity and density due to irregularity at the interface. The irregularity has been taken in the half- space in the form of a parabola. It is observed that Love waves propagate in this assumed medium. Irregularity and initial stress play an important role in the seismic wave propagation. This paper has been framed out to show the effect of irregularity at the interface in the parabolic form and initial stress on the propagation of Love waves. The presence of initial compressive stress reduces the velocity of Love waves. The numerical values of the phase velocity have been calculated using the values of material constants given by Biot [7] from experiments.

RESEARCH METHODOLOGY
I. The fluid inside the pores could be viscous. But in order to keep the analysis simple here, the material is assumed to be non-dissipative liquid filled porous solid; for instance, the water saturated rocks or grains.

II. The porous medium is assumed to have kinetic isotropy, but elastic anisotropy of Weiskopf type; the viscosity of water is neglected.

III. For upper layer μ =μ₀ (regidity) and p = p₀ (density) IV. The inhomogeneity in the half-space has been assumed to be of the form μ= μ₁(1 + mz ), p=p1 (1 +nz ) 
where, m and n are constants having dimensions that are inverse of length, ρ density and μ rigidity vary with space variable z, which is orthogonal to the xaxis i.e. direction of wave propagation.

V. It is assumed that the irregularity is of the form of a parabola with span of length 2 l and depth h. assuming the origin of the Cartesian co-ordinate system at the middle point of the interface irregularity and the z-axis downward positive.

VI. The equation of irregularity has been taken as,

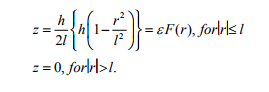
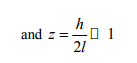
FORMULATION OF THE PROBLEM
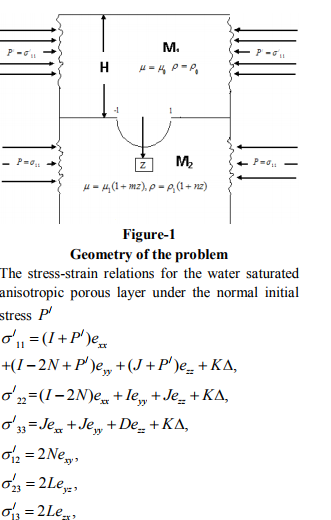
Consider a water saturated porous layer of thickness H with anisotropy of the Weiskopf type under the compressive initial stress along the direction of x over a non-homogeneous elastic half space under the compressive initial stress as shown in Fig.1 The wave is assumed to propagate along the x-direction. Neglecting the viscosity of water, the dynamic equations of motion in the porous layer under the compressive initial stress in the absence of body forces, can be written as;

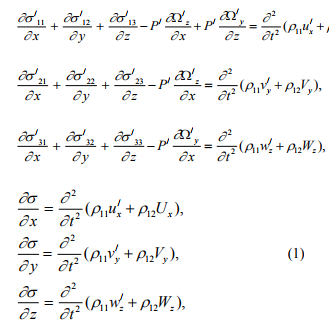
where, ? _ij ( i,j 1,2,3.....),  the incremental stress components, x y z u v w = the components of the displacement vector of the solid, U V W x y z = the components of the displacement vector of the liquid, ? _ij = the stress vector due to the liquid.

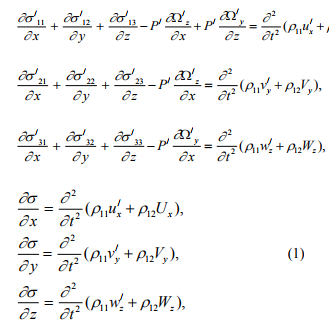
where, ?¹ _x  , ?¹ _x y and ?¹ _z are the components of the rotational component ? The dynamic Eq. (1) has been constructed by coupling the Biot’s dynamic equations in initially stressed medium and dynamic equations for a poroelastic medium.

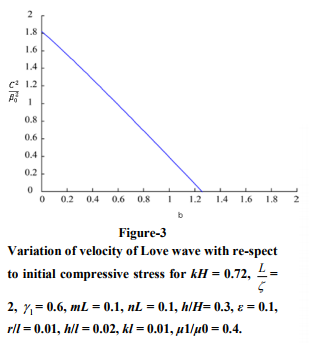
b) Figure 3 gives a variation of velocity of Love waves for the variation of 1 ? the curve confirm that as the initial stress parameter increases, the velocity decreases.

c) Figure 4 gives a variation of velocity of Love waves for the variation of porosity. The curve confirms that as the porosity increases, the velocity decreases.

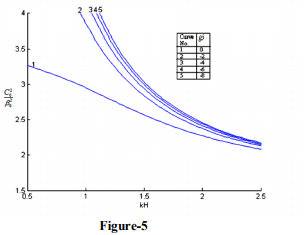
d) In Figure 5 the effect of tensile initial stresses ( 0) ?? in the half-space, in the absence of initial stresses in the porous layer, is shown. The curves show that the tensile initial stresses in the half-space increase the velocity of Love waves remarkably at low frequency; for compressive initial stresses in the halfspace, the Love waves do not propagate.

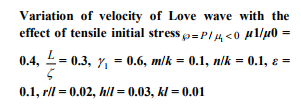
CONCLUSIONS
The effect of irregularity and the initial stresses are very prominent on the propagation of Love waves. The presence of initial compressive stress reduces the velocity of Love waves.As the porosity of the layer increases, the phase velocity of Love wave increases. As the anisotropy increases, the velocity of Love waves in the porous medium decreases. An increase in compressive initial stresses in the porous layer decreases the velocity of Love waves.

ACKNOWLEDGEMENTS
The authors convey their sincere thanks to DIPS Polytechnic College, for facilitating us with best facility. The authors are also thankful to the referees for their valuable comments

References:

1. Rayleigh, L. 1885. Waves propagated along the plane surface of an Elastic solid, Proc. Lond. Math. Soc., 4-11.

2. Love, A.E.H., (1911), “Some problems of geodynamics”, Combridge university press.

3. Ewing, W. M., Jardetzky, W. S., and Press, F., (1957), “Elastic Waves in Layered Media, McGraw-Hill”, New York

4. Vrettos, C. 1990 In plane vibrations of soil deposits with variable shear modulus, Int. J. Numer. Anal. Meth. Geomech, 14: 209–222.

5. Kennett, B. L. N. and Tkal?cic′, H. 2008. Dynamic Earth: crustal and mantle heterogeneity. Aust. J. Earth Sci., 55: 265– 279

6. Anderson, D.L. 1962. Love waves dispersion in heterogeneous anisotropic media. Geophysics, 1: 445-454.

7. Biot, M.A. 1956. Theory of elastic waves in fluid-saturated porous solid. J.Aconst. Soc. Am., 2: 168-178.

8. Staneley, R. 1924. Elastic waves at the surface of separation of two solids. Proc. Ray. Soc. Lond., 416-428.

9. Scholte, J.G.J. 1961. Propagation of love waves in inhomogeneous media. Geophys. Prosp., 87-116.

10. Chattopadhyay, A. ,Gupta, S., Singh, A. K and Sahu, S. A. 2010. Propagation of SH Waves in an irregular non homogeneous monoclinic crustal layer over a Semi-Infinite Monoclinic Medium Applied Mathematical Sciences, 4(44): 2157 – 2170

11. Sinha. N.K. 1966. Propagation of Love-waves in a non-homogeneous stratum of finite depth sand-witched between two semi-infinite isotropic media. PAGEOPH, 37-42.

12. Gogna, M.L., 1976. “Love waves in heterogeneous layered media”, Geophysc. J.R. Astr. Soc., pp 357-370.

13. Chadwick. P. 1993. The wave propagation in compressible transversely isotropic media. Proc. Roy. Irish. Acad. Sect. A, 93: 231-253.

14. Zhang, Z.M. 1998. Propagation of Love waves in transversely isotropic fluid saturated porous layered half space. J. Acoust. Soc. Am., 1: 695-701.

15. Dey, S. and Mahto, P. 1992. The effect of presence of rigid boundary in propagation of Love waves in sandwitched medium. Proceedings of Indian National Science Academy, 58, pp. 63-68.

16. Wilson, J.T. 1942. Surface waves in a heterogeneous medium. Bull. Seismo. Soc. Am., 1: 297-304.