IJCRR

IJCRR - 5(5), March, 2013

Pages: 71-88

Date of Publication: 22-Mar-2013

CALCULATING ESR PARAMETERS (H^& ?E h f) OF 4d AND 5d TRANSITION METAL ION COMPLEXES: A DFT STUDY.

Author: Harminder Singh A.K. Bhardwaj, M.L.Sehgal, Susheel K. Mittal

Category: General Sciences

Abstract:Density functional theory implemented in ADF 2009.01 was used to calculate the values of two ESR parameters namely effective spin Hamiltonian [H^] and hyperfine coupling energy (?E hf) along with the values of four factors (g, a, Q, and I) which contribute to the total value of the Hamiltonian for 45 complexes of six congeners of 2nd and 3rd transition series metal ions such as Zr (III) , Hf (III) ; Nb (IV), Ta(IV) ; Mo(III), W(III) ; Tc (II), Re(II) ; Ru (III), Os(III) ; Rh (IV), Ir (IV). Four relations which hold good both in regular (Oh) as well as distorted stereochemistries (D6h, D3d, D12, C2v, C1, C2) of these complexes were applied. The basis sets used were DZ or TPZ. The complexes were optimized to obtain ESR (g11, g22, g33, giso ; a11, a22, a33, A ten) and NQR parameters [?; q11, q22, q33 and NQCC] which were then used to calculate [H^] and [?Eh f].

Full Text:

INTRODUCTION
Effective spin Hamiltonian (H^) is a mathematical expression that determines energy of an ESR transition in a paramagnetic complex. The Hamiltonian depends upon a number of ESR parameters [anisotropic and isotropic splitting factors (g11, g22, g33, g iso ), hyperfine coupling constants (a11, a22, a33, Aten)], NQR parameters [electric field gradient or efg (q11,q22,q33), Nuclear Quadrupole Constant (Q)]1 , total electronic spin (S), Bohr Magneton of both the electron (?e) and of the nucleus (?n), nuclear spin quantum number (I), gn (nuclear magnetic ratio) along with nature of the surrounding nuclei if they possess quadrupole moments (I?1). 1 Q or e Q is the nuclear quadrupole moment. q Or e q is the electric field gradient. The product of the quantities (e Q × e q= e2Qq) is nuclear quadrupole coupling constant (Q). When certain commands were given to the ADF 2009.01, we obtained two ESR parameters (isotropic and anisotropic g, a) and three NQR [asymmetric coefficient (?), anisotropic electric field gradient or efg (q), nuclear quadrupole coupling constant or NQCC (Q)] parameters and optimization parameters of complexes. The three (g, a, Q) of these five parameters were used to calculate another two ESR parameters [effective spin Hamiltonian (H^) and hyperfine coupling energy (?E h f)] of complexes. The need for taking up this study arose because not much work was reported (1-29) on ESR studies of 4d and 5d metal ion complexes. In fact, theoretical calculation of Effective Spin Hamiltonian (H^) on such a vast number of complexes was never reported before because: (i) High values of spin orbit coupling constants (λ metal ion) of these metal ions would not allow exact determination of the ESR parameters experimentally. (ii) Cryoscopy conditions generally needed in low energy microwave region (X band: 9000- 10000 MHz) were difficult to obtain and cumbersome to maintain. The relevance and the objective of present work lied in the fact that simply by applying DFT (30-31) to ADF 2009.01; we were able to do away with all these limitations. Four relations were selectively used to calculate H^ and ?E h f parameters of 45 complexes such as [ZrX6] 3- (X=Cl , Br), [HfX6] 3- (X=F ,Cl, Br ), [Hf (NH3)6] 3+ , [Nb (NH3)6] 4+ , [NbX6] 2- (X=F ,Cl, NCS ), [TaX6] 2- (X= Cl, Br), [MoX6] 3- ( X=F, Cl ,Br, NCS), [Mo(OH2)6] 3+,[Mo(NH3)6] 3+ [WX6] 3- (X=F,Cl ,Br), [ W(OH2)6] 3+ , [W(NH3)6] 3+ , [TcX6] 4- (X= Cl ,Br, NCS) , [Tc (NH3)6] 2+, [ReX6] 4- (X= Cl ,Br), [Re(NH3)6] 2+ , [RuX6] 3- (X=F, Cl ,Br), [OsX6] 3- (X=F, Cl ,Br), [Os(NH3)6] 3+, [RhX6] 2- (X=F, Cl ,Br), [Rh(NH3)6] 4+ , [IrX6] 2- ( X=F, Cl ,Br), [Ir (NH3)6] 4+ .\

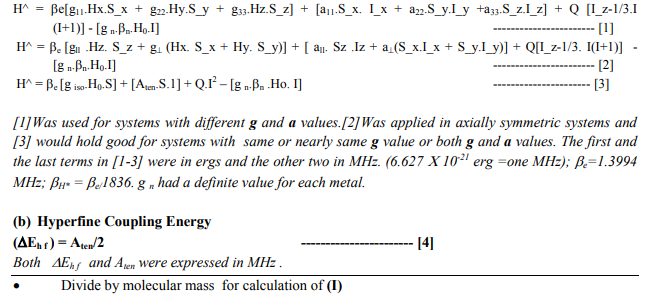
METHODOLOGY
After optimization of the complexes by ADF 2009.01, the software was run by applying Single Point, LDA? , Default, Spin Orbit, Unrestricted, None and Collinear commands by using DZ* or TPZ* Basis sets in all the 45 ? Acronyms are: LDA (Local Density Approximation); DZ (Double Zeta) TPZ (Triple Zeta) GGA BP (Generalized Gradient Approximation Becke Perdew); Nysom (Normalized) complexes except for [Os (NH3)6] 3+ and [Rh(NH3)6] 4+ where LDA was replaced by GGABP*. Each complex with NYSOM* symmetry generated an OUTPUT file of its own. It contained values of ESR (g11, g22, g33 and giso; a11, a22, a33 and A t e n), NQR (?, q11, q22, q33, NQCC) and optimization [geometry, dipole moment, bonding energy, total energy (X c) parameters having contributions from LDA and GGA*components; each being further made up of Exchange and Correlation parts].The bonding energy was computed as an energy difference between the molecule and fragments. As the fragments were single atoms, they were usually computed as Spherically Symmetric and SpinRestricted. So this usually did not represent the true atomic ground state (53-54) .
RESULTS
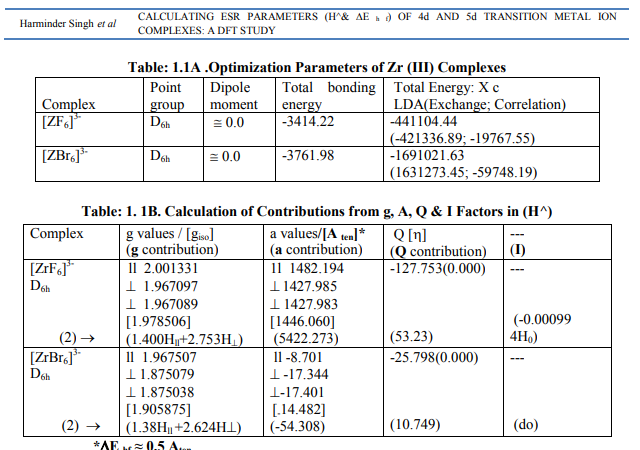
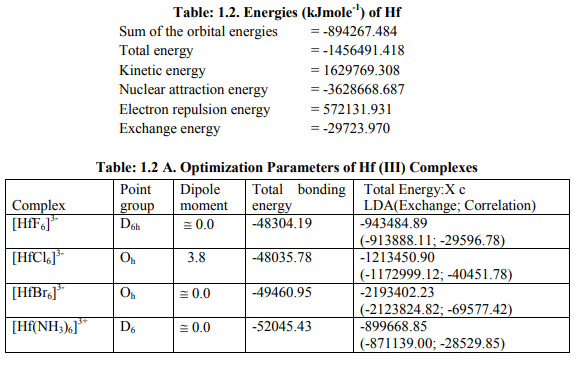
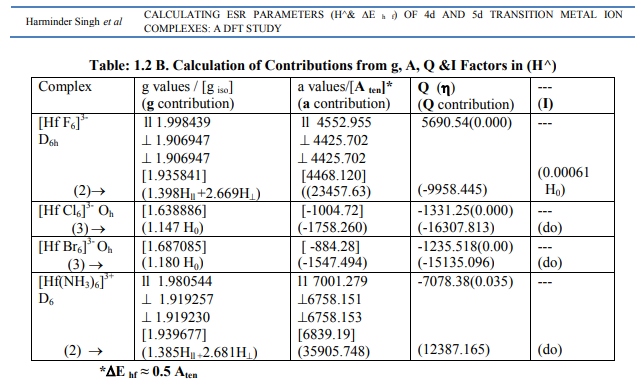
Tables: 1.1-1.12 and1.1-1 A-1.12A gave values of optimization parameters of 12 metals of the 2 nd and 3rd transition series and their 45 complexes respectively. Tables: 1.1B - 1.12B contained ESR and NQR parameters like g?, g ? ? , g iso; a? , a11, A ten and Q along with contributions from their respective factors. It also contained contribution from the fourth factor called interaction of nuclear magnetic moment with external magnetic field factor (I) in H^. These tables also gave ? E h f values of the complexes as calculated by [4]. [I] Calculation of H^ for Zr (III) and Hf (III) Complexes (a) [ZrX6] 3- (X = F, Cl) in Table: 1.1B were of axial symmetry with (a) two of the three g called g? being the same and the third of higher value was called g?? . (b) Two of the three a called a? were of same value and the third of higher value was called a11. (c) Two values of q out of the three were the same (d) ?=0. Relation [2] was applied to calculate their H^. (Put S_x=S_y=S_z=1/2; I_x=I_y=I_z=2.5 and g n= -0.5214480). (b) The Hf (III) complexes were categorized as follows (Table: 1.2 B): (i) [Hf X6] 3- (X=F, Br) had an axial symmetry with (a) two of the three g called g? being the same and the third with higher value was called g?? . (b) Two of the three a called a? being the same and the third with higher value was called a11. (c) Two of the three q values were the same. (d) ?=0. Relation [2] was applied to calculate their H^. (ii) In [Hf Cl6] 3- , all g and a parameters possessed same values respectively. Relation [3] was applied to calculate its H^. (iii) As g and a values respectively differ in [Hf (NH3)6] 3+, the relation [1] was used to calculate its H^. (Put S_x=S_y=S_z=1/2; I_x=I_y=I_z=3.5 and g n= 0.2267143). Individual contributions from the four factors in the total value of H^ for these six complexes were given in small brackets of horizontal row shown at the bottom (?) of Tables: 1.1B, 1.2B). (c) ? Eh f values of these Zr (III) and Hf (III) complexes were calculated by [4] (Tables: 1.1 B, 1.2 B).

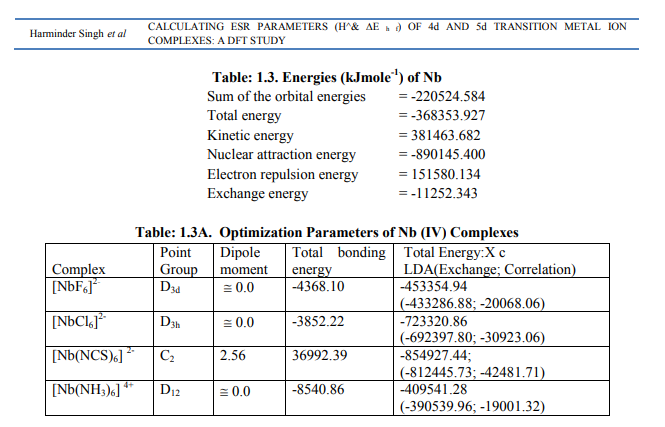
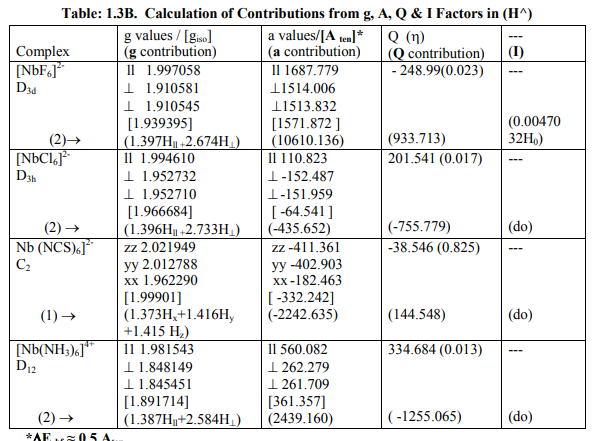
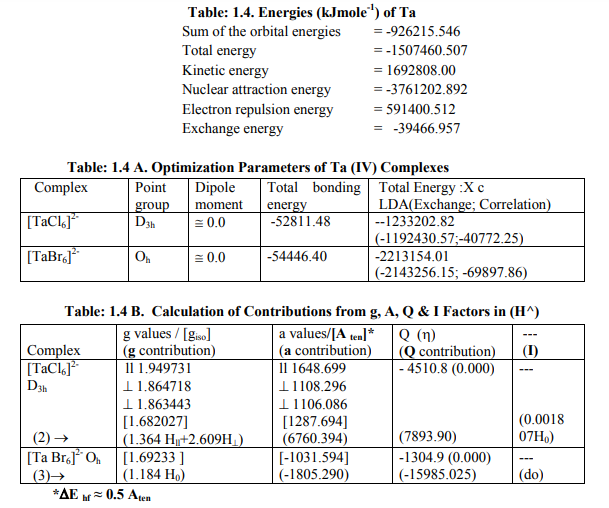
[1I]Calculation of H^ for Nb (IV) andTa (IV) complexes: (a) The complexes of Nb (IV) were categorized as follows (Table: 1.3 B): (i) [NbX6] 2- (X = F, Cl) and [Nb(NH3)6] 4+ were of axial symmetry with (a) two of the three g being the same called g? and the third with higher value was called g??. (b)Two of three a called a? being the same and the third of higher value was called a11. (c) Two of the three q values were of the same magnitude. (d) ?= 0. Relation [2] was applied to calculate their H^. (ii) [Nb (NCS) 6] 2- had different values of both g and a respectively. Relation [1] was applied to calculate its H^. (Put S_x=S_y=S_z=1/2; I_x=I_y=I_z= 4.5 and gn= 1.3712222). (b) The Ta (IV) complexes were categorized as follows (Table: 1.4 B): (i) [Ta Cl6] 2- had an axial symmetry with (a) two of the three g called g? being of same value and the third of higher value was called g?? . (b) Two of the three a called a? being of the same value and the third of higher value was called a11. (c) Two of the three q were of same value. (d) ?=0. Relation [2] was used to calculate H^. (ii) [Ta Br6] 2- possessed almost same values of g and a. Relation [3] was applied to calculate its H^. (Put S_x=S_y=S_z=1/2; I_x=I_y=I_z=3.5 and gn= 0.6772857). Individual contributions from four factors in the total value of H^ for these six complexes were given in small brackets of horizontal row shown at the bottom (?) of Tables: 1.3 B, 1. 4B). (c) ?Eh f for these Nb (IV) and Ta(IV) complexes was calculated by [4] (Tables: 1.3 B, 1.4 B).

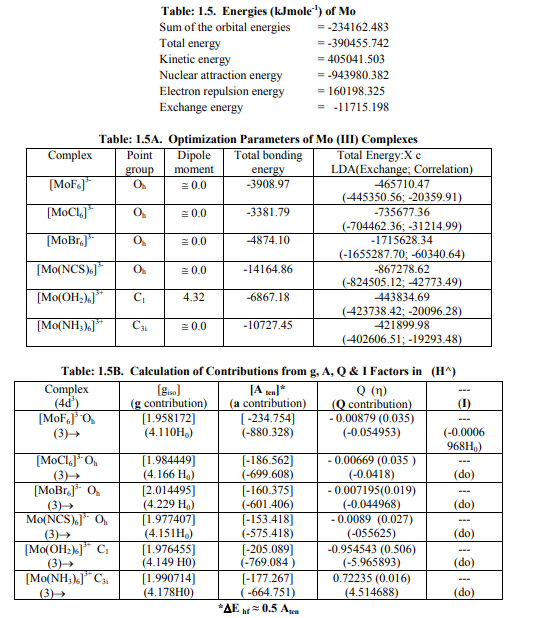
[1II] Calculation of H^ for Mo (III) andW (III) complexes: (a) All the six Mo (III) complexes (Table: 1.5 B) such as [MoX6] 3- (X=F, Cl, Br, CNS) as well as [Mo (OH2)6] 3+and [Mo (NH3)6] 3+ had nearly the same values of a and g parameters. Relation [3] was applied to calculate their H^. (Put S_x=S_y=S_z=3/2; I_x=I_y=I_z=2.5 and g n= -0.3656800). (b) All the five W (III) complexes (Table: 1.6 B) like [W X6] 3- (X=F, Cl, Br) as well as [W (OH2)6] 3+ and [W (NH3)6] 3+ possessed nearly the same values of g and a parameters. Relation [3] was applied to calculate H^ for all these complexes. (Put S_x=S_y=S_z=3/2; I_x=I_y=I_z=0.5 and g n= 0.2355696). Values of individual contributions from the four factors in the total value of (H^) for these eleven complexes were given in small brackets of a horizontal row shown at the bottom of each complex (?) of Tables: 1. 5 B and 1.6B. With I=0.5, there is no NQCC for W (III) complexes. Therefore, only three factors would contribute in the total value of H^ in its complexes. (c) ?E hf for these Mo (III) and W (III) complexes was calculated by [4] (Tables: 1.5 B, 1.6 B).