IJCRR

IJCRR - 5(6), March, 2013

Pages: 01-06

Date of Publication: 30-Mar-2013

PERSISTANCE ANALYSIS OF AEROSOLS AND ITS IMPACT ON RAINFALL QUANTITY AT CHENNAI

Author: K. Padma, R. Samuel Selvaraj, B. Milton Boaz

Category: General Sciences

Abstract:Aerosol plays an important role in the radiation budget of Earth's atmospheric system. They serve as cloud condensation nuclei and have a substantial effect on cloud properties. Large concentrations of human made aerosol have been reported to decrease the rainfall as a result of their radioactive and Cloud condensation Nucleus (CCN) activities. On the other hand, heavily polluted clouds evaporate much of their water before precipitation could occur. This paper concentrates at Chennai (13o 04' N 80o 17' E), situated in the north east of Tamil Nadu on the coast of Bay of Bengal. Aerosol generated in urban areas can act to suppress rainfall which inhibits the collision and coalescence process. Moreover, increased, decreased trend of rainfall quantity recorded during the years 1987 - 2009 on this coastal urban area had been analyzed. Correlation Coefficient between aerosol and rainfall quantity were found using Spearman Rank Correlation technique. Hurst exponent had also found to study the behavior of aerosol concentration on the 262 days time series data observed over the year 2010.

Keywords: Aerosol, rainfall quantity

Full Text:

INTRODUCTION
Aerosol is extremely fine liquid droplets or solid particle; those remain suspended in the air. Small aerosol particles affect the natural energy balance of the earth mainly by reflecting (and in some cases absorbing) solar radiation. The radiative and microphysical impacts of aerosols affect the cloud composition, precipitation, hydrological cycle and the atmospheric circulation system. Troposphere aerosols are important in determining cloud properties, but it has been difficult to quantify their effect because they have a relatively short lifetime and vary strongly in space and time (Madhavi Latha et al., 2003). This atmospheric study on the variation of aerosol concentration in relation to metrological parameters, are important to characterize number of phenomena occurring in the lower troposphere (Deepti Saxena et al.2010). Aerosols of both natural and anthropogenic origins play a crucial role in cloud formation and the atmospheric hydrologic cycle. During the past few decades, anthropogenic emission of aerosol precursors has increased considerably because of the increase in industrial activities (Cheng et al. 2005, Gong et al. 2007). The corresponding increase in anthropogenic aerosol would act as a superfluous forcing to alter atmospheric physical process such as radiation, the size spectrum of cloud particles, cloud cover, atmospheric stability, and precipitation (Youg-Sang 2007, Ramanatha et al.2001, Kaufman et al. 2005. Aerosol concentration affects the rainfall in several ways. Direct aerosol effect consists of direct interaction of radiation with atmospheric aerosol, such as absorption or scattering. It produces net radiative forcing and magnitude of the net resultant radiative forcing dependent on the albedo of the underlying surface, as this affects the net amount of radiation absorbed or scattered to space. Due to this effect aerosols on clouds mostly act to suppress precipitation because they decreases the amount of solar radiation that reaches the land surface and therefore causes less heat to be available for evaporating water and energizing convective rain clouds. In addition to that which decreases clouds layers by heating the air and reducing relative humidity where aerosol absorption is strong (Johnson et al. 2003, Penner et al., 2006). Moreover the direct radiative effects of aerosol i.e., the extinction of sunlight by aerosol scattering and absorption can cause changes clouds through changes in temperature structure of atmosphere (termed the semi-direct affect of aerosols on clouds) (Penner et al. 2006). First indirect effect relates to an increase in aerosol particles may increase the initial cloud droplet number concentration if the cloud liquid water content is assumed constant. This effect tends to cool the climate because it increases the cloud optical depth due to change in the cloud droplet number will lead to decrease the size of the cloud droplet ( Penner et al. 2006,Towmey1974). The second indirect effect relates to cloud morphology associated with changes in the precipitation efficiency of the cloud. But the cloud microphysical process that form precipitation depend on the size of the droplet, the cloud life time as well as the liquid water content, the height of the cloud and the cloud cover may increase through the change in droplet number concentration which is sensitive to the meteorological condition. (Ackerman et al.2004). Moreover aerosol incorporated in orographic clouds slow down cloud-drop coalescence and riming on ice precipitation and hence delays conversion of cloud water precipitation. (Amir Givati, et al. 2004). Finally aerosol mixed up into cloud it affects cloud microphysical properties in the anticipated ways increasing cloud droplet number concentration and decreasing droplet effective radius as well as size. The need for broad droplet distribution with a significant population of cloud droplets larger than about 15µm for precipitation to occur efficiently in warm clouds and the polluted clouds having small droplets and narrow droplet size distribution might be less efficient in production of rain. (Ackerman et al.2004). Aerosol particles through their enhancement of clouds may reduce the near surface wind speeds. Slower winds and cooler surface temperature also reduces the moisture advection evaporation. These factors along with the second indirect aerosol effect may reduce precipitation (Mark Z. Jacobson et al. 2006). The winds that blow near the surface of the Earth have two beneficial effects. They provide a renewable source of clean energy and they evaporate water, helping rain clouds to build up. According to Stanford and NASA researches aerosolized particles created from vehicle exhaust and other contaminants can accumulate in the atmosphere and reduce the speed of winds closer to the Earth’s surface which results in less wind speed and also reduced precipitation. Thus increase in aerosol concentrations, via aerosol indirect and semidirect effects, may affect the long-term variations in precipitation in conjunction with other climatic conditions such as global warming. Hence aerosol concentration and precipitation, rainfall are closely related with each other (Mark Z. Jacobson 2006)

DATA AND METHODOLOGY
This study investigates the relationship between aerosol concentration and rainfall quantity at Chennai using daily surface observations of particulate matters (PM10) concentration. Aerosol data has been obtained from Pollution Control Board at Guindy, Chennai. Rainfall data for the corresponding years are obtained from Regional Meteorological Centre, Chennai. Correlation coefficient is found using Spearman Rank Correlation method. The persistence behavior of the aerosol data has been studied by finding Hurst exponent.

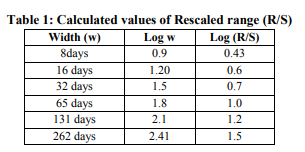
The Spearman Rank Correlation (ρ) is a nonparametric measure of statistical dependence between two variables. It is a test for correlation using ranked data. As we use the rank order than the actual values for determining the association between the two set of (aerosol and rainfall) values it is called a “rank correlation.” The actual data are ranked, usually in ascending order i.e., a rank order 1 is allotted to the smallest values of each variable in x and y. The rank order n is given to the largest variable. If two or more values of the variable x and y are tied, they are each assigned the average of the rank positions otherwise they would have been assigned individually if ties had not occurred. For each of the n values of the variables, a set of rank difference is obtained, d = Rx - Ry as the sum of the difference in rank of paired values is zero i.e., ∑d=0, we use ∑d2 . Finally Spearman Rank Correlation (ρ) is ρ = 1- (6 ∑d2 /n3 -n) Where n is the number of data considered and d is the difference between the ranks of each observation on the two variables. The rank correlation coefficient is a relative measure which varies from -1 through 0 to +1. The Hurst exponent is used as a measure of the long term memory of time series, i.e. the autocorrelation of the time series. To calculate the Hurst exponent, estimation of the dependence of the rescaled range on the time span n of observation is very important. A time series of full length N is divided into a number of shorter time series of length n = N, N/2, N/4... (In our study total number of data is 262. It divided into two sets of 131 each (N/2) then it is further divided into four sets of 65 each (N/4) and so on.) The average rescaled range is then calculated for each value of n. Computing (R/S) (t0, w) for time lag w the rescaled range for the time lag w is finally written as the average of those values (Here R, S are calculated for each time series of n). It has been observed that the rescaled range (R/S) over a time window of width w varies as a power law: (R/S) w = k WH, where k is a constant and H is the Hurst exponent. To estimate the value of the Hurst exponent, R/S is plotted against w on log-log axes. The slope of the linear regression gives the value of the Hurst exponent. A value of 0 < H < 0.5 indicates a time series with negative autocorrelation (e.g. a decrease between values will probably be followed by an increase), and a value of 0.5 < H < 1 indicates a time series with positive autocorrelation (e.g. an increase between values will probably be followed by another increase). A value of H=0.5 indicates a true random walk, where it is equally likely that a decrease or an increase will follow from any particular value (e.g. the time series has no memory of previous values). In addition to that the H exponent vary between 0 and 1, with higher values indicating a smoother tend, less volatility and less roughness. The Hurst exponent is related to the fractal dimension D of the time series curve by the formula, D=2-H, D=2-0.6998=1.3002 When the fractal dimension, D for the time series is 1.5, there is no correlation in amplitude change between two successive time intervals and is unpredictable. When dimension decreases to 1 the process becomes more and predictable, when fractal dimension increases from 1.5 to 2 the process exhibit anti persistent. RESULT AND

DISCUSSIONS
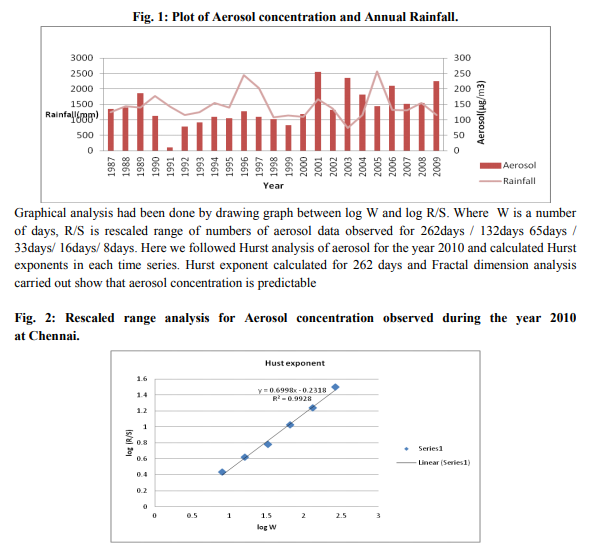
The relationship between aerosol concentration and annual rainfall at Chennai has been found using Spearman Rank correlation. The Correlation Coefficient was found to be - 0.199. The aerosol concentration affects the quantity of rainfall to some extend at Chennai. The decreasing trend of the annual rainfall quantity due to the increase in aerosol concentration has been illustrated in fig. 1. The Hurst’s exponent for the concerned aerosol concentration data was found to be 0.699 as shown in fig. 2. The rescaled range (R/S) values are tabulated in table 1. This shows the persistence behavior of it. The Fractal Dimension, D was found to be 1.3002. Aerosol concentration has been increased in Chennai accompanied by a decrease in rainfall events over the last few years. Aerosol concentration has been abruptly increased in the years 1989, 2001, 2003, 2006 and 2009 and decreased in 1991, 1999, 2002 and 2005. On the contrary, the rainfall quantity attained lower heights in the years 1987, 1993, 2000 and 2003 and greater heights in the years 1990, 1996, 2001 and 2005. Insufficient rainfall witnessed in the years 2003. . Further from the graph we can understand aerosol concentration well correlated to rain fall in some years. This result show that increasing aerosol load affects the cloud produces less rain at few individual times some cases were turned when polluted convective clouds produced intensified rainfall via mixed microphysics (Yong-San Choi et.al., 2007). More over since many factor affect precipitation formation and rain fall in urban areas, is difficult to reveal and to quantitatively evaluate effect of aerosol in these areas.

CONCLISION
At the time of our study we were able to collect 23 years (1987-2009) monthly data and 2010 daily data only. From our study we found that the relation between aerosol concentration and rainfall. It shows increasing aerosol concentration affect the cloud development and causes less rainfall in some extend. Furthermore we used 262 days aerosol data and employed R/S method to compute Hurst exponent H and fractal dimension analysis also carried out. It shows the aerosol concentration in time series is predictable. It means that a time series with long – term positive autocorrelation both high value in the series will probably be followed by another high value and that the values a long time on to the future will also tend to be high.

ACKNOWLEDGEMENT
The authors would like to thank Pollution Control Board, Regional Meteorological Centre, Chennai for providing rainfall datat and pollutants data. Authors acknowledge the great help received from the scholars whose articles cited and included in references of this manuscript. The authors are also grateful to authors / editors / publishers of all those articles, journals and books from where the literature for this article has been reviewed and discussed. Authors are grateful to IJCRR editorial board members and IJCRR team of reviewers who have helped to bring quality to this manuscript.

References:

1. Madhavi Latha. K., Krishna Prasad. V and Badarinath.K.V.S. 2003. Aerosol characteristic and radiative forcing over industrial areas of urban environment – A case study from Hyderabad and its environs. J. Ind. Geophy. Union (2003), Vol.7. No, pp.25-29.

2. Deepti saxena, R.Yadav, Adarsh kumar and Jagdish Rai, 2010. Measurement of atmospheric aerosol during monsoon and winter seasons at Roorkee, India, Indian journal of Radio & space physics, Vol.39.

3. Cheng, y., Lohmann, U, Zhang, J., Liu, Y. and Lesins. G, 2005. Contribution of changes in sea temperature and aerosol loading to the decreasing precipitation trend in southern China, Jr. Climate, 18, 1381-1390.

4. Gong, D.Y.and C.H.Ho, 2007. Shift in the summer rainfall over the Yangtze aaariver valley in the late 1970s, Geophy. Res. Lett. 29, 1436.

5. Yong-Sang Choi and Chang-Hoi Ho, Jinwon Kim, Dao-Yi Gong, Rokjin J.Park 2007. The impact of Aerosols on the summer rainfall frequency in China, Journal of Applied meteorology and climatology, Vol.47, pp. 1802-1813.

6. Ramanathan, Crutyzen V.P.J, Kieh J. Tl., and Rosenfield.D. 2001. Aerosols, climate, and the hydrological cycle, Science, 294, 2119- 2124.

7. Kaufman, Koren Y. J. I, Remer, D. Rosenfeld L. A., and Rudich.Y. 2005. The effect of smoke, dust and pollution aerosol on shallow cloud development over the Atlantic Ocean. Pro. Natl. Acad. Sci. USA, 102, 11207- 11312. 

8. Johnson et al. B.T., 2003. The semi–direct effect: Impact of absorbing aerosol on marine stratocumulus, Q. J. R. Meteorol. Soc. 130, 1407 – 1422

9. Penner J.E., QWuaas J., Storelvma T.,Takemura.,T.,.Boucher Kirkevag .K, Kristijansson J.E., and Seland O..2006. Model intercomparison of indirect aerosol ffects.,A tmos.Chem.Phys,Vol.6.3391-3405.

10. Twomey. S., 1974. Pollution and the planetary albedo, Atmos, Environ. 8, 1251- 1256.

11. Ackerman, A. S., Kirkpatrick, M. P., Stevens, D. E., and Toon, O. B, 2004. The impact of humidity above sraitiform clouds on indirect aerosol climate forcing, Nature, 1014-1017.

12. Amir Givati and Daniel Rosenfield, 2004. Quantifying precipitation suppression due to Air Pollution, AMS Journals online, Vol. 43, issue7.

13. Mark Z. Jacobson and Yoram J, Kaufman. November 2006. Wind reduction by aerosol particle. Geo Physical letters, Vol. 33.