IJCRR

IJCRR - 5(4), February, 2013

Pages: 141-147

Date of Publication: 28-Feb-2013

ENCRYPTION AND DECRYPTION USING ANGLES

Author: M. Yamuna, Kailash Chandra Sanwal, Radhe Shyam Jangid, Sanyam Jain

Category: Technology

Abstract:In this paper we provide a method of encryption and decryption of messages using properties of angles in a circle. We have devised a method of developing a base chart using concentric circles and hence encrypt and decrypt any message. The base chart and the angle of the circle is used as the encryption decryption key.

Keywords: Circle, Angle.

Full Text:

INTRODUCTION
Encryption is a process which is applied to text messages or other important data, and alters it to make it humanly unreadable except by someone who knows how to decrypt it. Encryption is a method by which any kind of messages such as email, e-commerce, banking, or any other personal information, become encoded so they are illegible to anyone other the intended person without a special deciphering of the code, with a special key or other code. This form of security is necessary to handle the privacy of almost all personal and private information Encryption Decryption Key that passes through from one computer to another. Information such as data or messages that are sent is regarded as plain text until that information is encrypted and then is labeled as Cipher text. [ 4 ] Encryption becomes vital for a secure and safe environment for the computers and the internet. In cryptography, encryption is the process of encoding messages ( or information ) in such a way that eavesdroppers or hackers cannot read it, but that authorized parties can. In an encryption scheme, the message or information ( referred to as plaintext ) is encrypted using an encryption algorithm, turning it into an unreadable cipher text. Decryption is the reverse process to encryption. Frequently, the same Cipher is used for both encryption and decryption, while encryption creates a Cipher text from a plaintext, decryption creates a plaintext from a Cipher text. [5] In this paper we propose a method of encryption and decryption of any message, using the properties of angles in a circle as the key for encryption and decryption.

MATERIALS AND METHOD
A circle can be defined as the curve traced out by a point that moves so that its distance from a given point is constant. A sector is a region bounded by two radii and an arc lying between the radii. A chord is a line segment whose endpoints lie on the circle. Diameter of a circle is the longest chord, a line segment whose endpoints lie on the circle and which passes through the centre; or the length of such a segment, which is the largest distance between any two points on the circle. Concentric circles are circles with a common center. The region between two concentric circles of different radii is called an annulus. Any two circles can be made concentric by inversion by picking the inversion center as one of the limiting points. [ 2 ] The circle with its center at the origin is a platform for describing all the possible angle measures from 0 to 360 degrees, plus all the negatives of those angles, and plus all the multiples of the positive and negative angles from negative infinity to positive infinity. The positive angles on the unit circle are measured with the initial side on the positive -axis and the terminal side moving counterclockwise around the origin. If we measure angles clockwise instead of counterclockwise, then the angles have negative measures. [ 3 ]

MAIN RESULT
We first determine the number of symbols ( x ) required for encryption of any message. We then construct nine concentric circles to generate eight annulus. Let us label the annulus as A1, A2,…, A8, where A1 is the innermost annulus. We then divide these nine concentric circles into 360 / x parts with respect to the origin by drawing 360 / x diameters that is, all the concentric circles are divided into 360/ x sectors, where the angle of each sector is 360 / x. We fix the upper and lower limits for each angle of the sector. For the first sector we fix the lower limit as 0 and upper limit as 360 / x ( rounded off to nearest integer ). This is expressed as [ 0, 360 / x ]. We design the base chart as follows. We use the annulus for representing the angles and values. All the values in the chart are written in the counter clockwise direction. A1: Label for all the x symbols starting from 1. A2: The x symbols are inscribed in any random order of comfort. A3: The corresponding positive angles of each symbol is listed. A4: The values of the angles rounded off to the nearest integer value is listed. A5: The upper and lower limit values of the corresponding angles is listed. A6: The corresponding negative angles of each symbol is listed. A7: The values of the angles rounded off to the nearest integer value is listed. A8: The upper and lower limit values of the corresponding angles is listed. This base chart can be designed as per the need of the message to be encrypted. This base chart will be the key chart to be used for encryption and decryption that can be designed and decided by the transmitter and receiver depending on their need and use. Once the base chart is decided we decide the encryption key based on the positive or negative angles of the base chart. The message is then encrypted with the first symbol representing the encryption key using the upper lower limit values of the corresponding angles from the base chart.

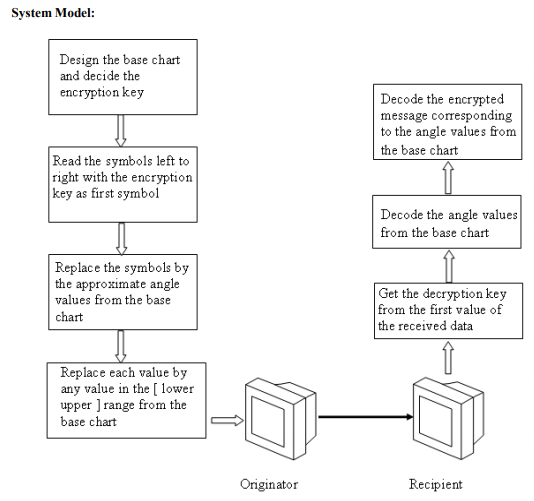
Model Chart:
For representation of the chart we choose 40 symbols which are necessary for encryption of a normal message. The number of symbols in the chart can be increased on decreased depending on the need of the message to be encrypted. All the forty sectors are represented in the chart where the angle of each sector is 9o . All the values of the eight annulus are listed as explained. The negative angles are listed without the negative sign.

Encryption Decryption Key
Apart from the encryption chart we also decide an encryption key. We provide four possible keys.

1. Key 1 = Positive angles. We shall use p as the encryption key in this case. In an encoded message the first symbol p indicates that the message is encoded using positive angles.

2. Key 2 = Negative angles. We shall use q as the encryption key in this case. In an encoded message the first symbol q indicates that the message is encoded using negative angles.

3. Key 3 = Positive negative angles. We shall use r as the encryption key in this case. In an encoded message the first symbol r indicates that the message is encoded using alternatively positive negative angles.

4. Key 4 = Negative positive angles. We shall use s as the encryption key in this case. In an encoded message the first symbol s indicates that the message is encoded using alternatively negative positive angles.

Encryption Algorithm

• Read the message symbol by symbol from left to right.
• Decide any one of the four encryption keys and add it as the first symbol of the message that is, the leftmost symbol will represent the decided key.
• Replace every symbol by its approximate angle value from the base chart. We assign a three digit value to all the symbols. For symbols with one or two digit angle values prefix the value with zeros.
• Replace every approximate angle value by any three digit angle value (one or two digit angle values are prefixed with zeros ) from the corresponding [ lower, upper ] range. ? Encrypted the angle values as the message.

Decryption Algorithm

• Get the encrypted message.
• From the first three digit values decide the encryption key from the base chart.
• Determine the corresponding symbols for the remaining angles using the base chart and encryption key decrypt the message.

Example
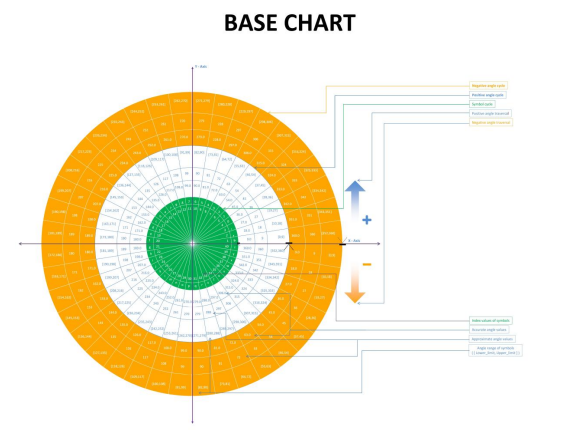
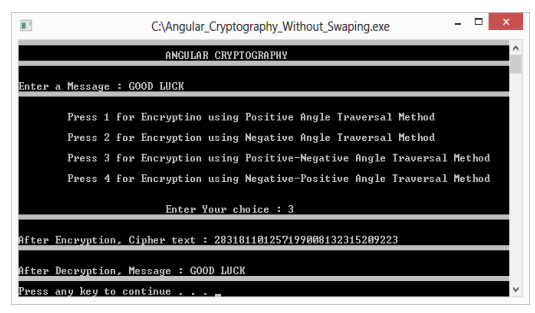
Suppose we want to send the message GOOD LUCK. Let us use the positive angle traversal. So the message to be encrypted is PGOOD LUCK. The approximate angle from the base chart is 270 189 261 261 162 9 234 315 153 225. The upper and lower limit angles angle ranges from the base chart is [ 262, 270 ] [ 181, 189 ] [ 253, 261 ] [ 253, 261 ] [ 154, 162 ] [ 0, 9 ] [ 226, 234 ] [ 307, 315 ] [ 145, 153 ] [ 217, 225 ]. Selecting any value from this range one possible way in which the data to be send is ( the data are separated by space ) 182260255159008233313150219 From the limits of the angles we observe that the there are 910 = 3486784401 ways of encoding the message GOOD LUCK. Suppose the received data is 084059170228115137069. Since the first value is 084 from the chart we observe that the decryption key corresponds to negative angle. Also from the chart we can calculate the received values fit in the range [ 55, 63 ] [ 163, 171 ] [ 226, 234 ] [ 109, 117 ] [ 136, 144 ] [ 64, 72 ]. From the chart the received data is decrypted as THANKS This proposed method can be programmed in any comfortable programming language. We have written a program in C++ using the model base chart with 40 symbols. Our output screen for one example is shown below.

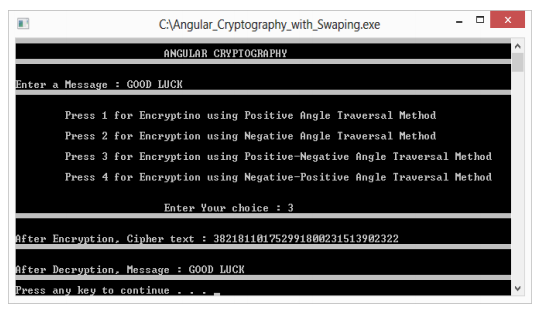
Before the message is transmitted we can also swap the three digit values. For example suppose the three digit angle value is 283. Then this can also be encoded as 238, 823, 832, 328, 382. This will avoid anyone from guessing that angles are used for encryption because now the upper limit of the three digit values is no more 360. For each three digit angle value we have 3! Ways of encryption. This infact increases the security of the system. For each of the 9 10 ways of encrypting the message GOOD LUCK we have 3!10 ways of sending the message by this swapping technique. We also have done a program by swapping the data. Our output screen for the same example with swapping is shown below

CONCLUSION
By using combinatory method with additional mathematical techniques (ex: swapping of each angles, some addition or subtraction etc.) it is becoming the most secure cryptographic technique. By doing a complete rotation or two (or more) and adding or subtracting 360 degrees or a multiple of it before settling on the angle’s terminal side, we can get an infinite number of angle measures, both positive and negative, for the same basic angle. We have used a circle to construct the base chart. We can use rectangles, squares, or any kind of polygons and their angles to prepare the base chart. So we conclude that apart from the method provided here to construct the base chart there are many other ways in which one can design the encryption decryption chart. The arrangement of the symbols in the annulus A2 can be done in x! ways. So the three digit angle values assigned to the symbols vary as the arrangement in the annulus A2 changes. Also as the number of symbols under consideration reduce, the number of combinations possible for [upper, lower] limits increases and hence the number of combinations available for encryption of the symbol increases. We can design the base chart with the required number of symbols and hence increase the security of the system. Also in the proposed method we have used only integer values. Use of real numbers for the [upper, lower] limit provides us infinite number of possible ways for encryption of a single symbol. All these advantages of this way of encryption ensure the safety of the encoded message making the proposed system a safe and efficient one.

ACKNOWLEDGEMENT
Authors acknowledge the great help received from the scholars whose articles cited and included in references of this manuscript. The authors are also grateful to authors / editors / publishers of all those articles, journals and books from where the literature for this article has been reviewed and discussed. Authors are grateful to IJCRR editorial board members and IJCRR team of reviewers who have helped to bring quality to this manuscript.

References:

1. Jin Ho Kwak, Sungpyo Hong, Linear Algebra, Second Edition, Springer International Edition.

2. http://en.wikipedia.org/wiki/Circle (accessed on 2012 Nov 05)

3. http://www.dummies.com/howto/content/negative-and-positive-anglescutting-a-circle.html. (accessed on 2012 Nov 05)

4. http://www.essortment.com/encryption29511.html [accessed on 2012 Nov 02].

5. http://en.wikipedia.org/wiki/Encryption. [accessed on 2012 Nov 02]