IJCRR

IJCRR - 5(11), June, 2013

Pages: 144-153

Date of Publication: 18-Jun-2013

PROPAGATION OF THE SHOCK WAVES IN THE EARTH'S ATMOSPHERE

Author: Rajan Singh, Mukesh Chandra, Kapil Kumar

Category: Technology

Abstract:Propagation of shock waves in non-uniform medium with various density distributions has been discussed. Plane shock waves as it propagates vertically upward in the static atmosphere of the earth are also studied. The variation of Mach number and the velocity of the shock waves are obtained analytically by using Whitham's Rule. It is found that shock velocity increases as the shock wave propagates in the atmosphere with decreasing density normal to plane of the shock front.

Keywords: Shock wave, pressure, density, velocity, Mach number, propagation, adiabatic and isothermal atmosphere.

Full Text:

1. INTRODUCTION
Bhatnagar and Sachdev [1] have obtained a relation between the density, pressure and Mach number by using Whitham's Rule to the propagation of the shock waves in the nonhomogeneous medium. Kopal and Carrus [2], Hardy and Grover [3] have been studied the problem of propagation of the shock waves in a non-uniform medium with various density distributions and found the behavior of the fluid flow in the presence of the shock waves. Hayes [4] investigated the vorticity jump across a gas dynamics discontinuity by considering the radiative heat transfer into account and concluded that for an optically thin gas, vorticity is unaffected in pseudo-stationary flows. Kanwal [5, 6] employed the theory of generalized functions and differential geometry to study the propagation and deformation of wave front in stationary three dimensional gas flows. With minor changes the experimental data for temperature distribution given by Mitra [8] has been used. In this paper, we have studied the problem of propagation of the shock waves in the earth's atmosphere and also used the Whitham's rule. The experimental data for temperature distribution given by Mitra [8] has been used for minor changes

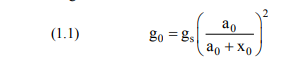
wherein a0 is the earth's radius, x0 is the vertical distance from the surface of the earth and s g is the value of g 0 at the surface of the earth. Using the variation of the Mach number of the shock and the different temperature distribution of the earth's atmosphere is obtained. The results are combined to find the variation of shock velocity as the shock propagates in the atmosphere. It is found that the shock velocity increases as the shock propagates into the medium which become rarer and rarer with the distance measured from the surface of the earth. As the shock velocity increases with the distance high velocity of the shock causes the fluid velocity to be greater than the escape velocity in the upper atmosphere. But at such a height, the density of the fluid is so small that every small quantity of the fluid escapes from the earth's gravity. Moreover the turbulent motion of the gases in the atmosphere and the effects of the magnetic field and solar radiation, which have not been taken into account, are disturbing the atmosphere. But in all the discussion leads us to a physical picture of the shock wave propagation in the earth’s atmosphere.

Let us assume that there is an intense explosion at the surface of the earth, due to which a strong shock wave propagates in the atmosphere. The radius of the earth is greater than the height of the atmosphere; therefore it can be considered that layers of the atmosphere are planer and the path of the shock wave is one dimensional. Taking X-axis to be normal to the surface of the earth, let gs , Ts , ps , ? s and go, To, po, ?0 be the acceleration, absolute temperature, pressure and density due to gravity at the surface of the earth respectively and at distance xo from the surface. The pressure variations in equilibrium conditions is given by [8]

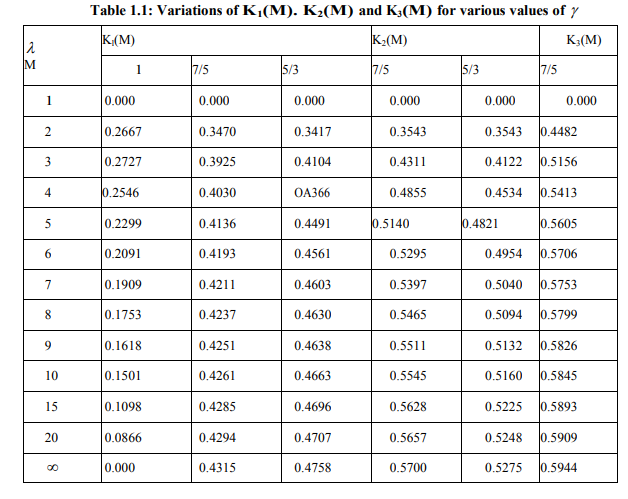
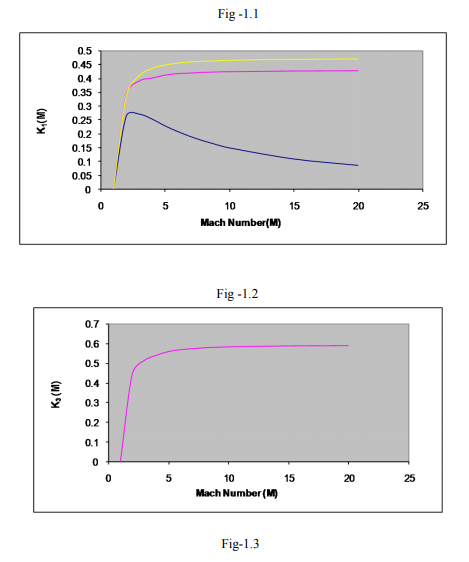
Wherein R is the distance of the shock front from the surface of the earth and c is the dimensionless sound velocity. The equation (2.8) gives the relation between p, c and M. If the absolute temperature is given, one can find pressure from equation (2.1) and M may be calculated from the relation (2.8). Now the atmosphere can be adiabatic or isothermal or the temperature may be monotonically increasing or decreasing in it. Therefore the relation (2.8) has been studied for different cases.

3. ADIABATIC ATMOSPHERE
The earth's atmosphere is extremely transparent to the radiation from the sun, and is hardly heated by it. Thus almost all the radiation from the sun falls on the surface of the earth. The radiation

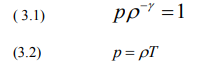
falling on the surface of the earth is reflected back to the atmosphere in the form of infrared rays. The infrared rays are absorbed by the carbon dioxide and water vapors in the lower part of the atmosphere. Thus near the surface of the earth, the temperature falls rapidly with the height. This rapid fall produces instability in the density of the atmosphere and there are strong airs current in this region. They stabilize the fluctuations in the temperature. As the rate of conduction of heat in the gases is very small, therefore an adiabatic equilibrium condition is setup. This state occurs in the troposphere. For the adiabatic atmosphere, one has in terms of the dimensionless pressure, density and temperature

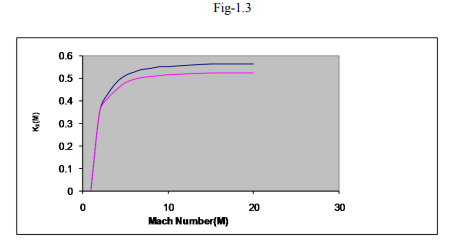
4. ISOTHERMAL ATMOSPHERE
In this case there .are no external forces acting on the atmosphere, there will be no motion of the air. Since conduction of heat from one part of the atmosphere to the other is slow in the absence of the external forces the atmosphere will attain uniform temperature after sufficient length of time. Let T1 be uniform dimensionless temperature, p1 be the pressure at r = r1 is the height of isothermal atmosphere from the surface of the earth, then the equation (2.1) reduces in the form

5. MEDIUM WITH MONOTONICALLY INCREASING TEMPERATURE
In the upper part of the atmosphere, ultraviolet rays of the sun cause some of the air to ionize, which combines with oxygen and forms ozone. Ozone is found at the height of 10 km. to 15 km. from the surface of the earth. It observes the heat of sun and thus the atmosphere is heated by it. The heat absorbed up to the height of 30 km. is negligible, but beyond 30 km. the temperature of the atmosphere starts

ACKNOWLEDGEMENT
Authors acknowledge the immense help received from the scholars whose articles are cited and included in the manuscript. The authors are also grateful to authors / editors / publishers of all those articles, journals and books from where the literature for this article has been reviewed and discussed. Authors are grateful to IJCRR editorial board members and reviewers for their useful comments that lead the improvement of the manuscript.

References:

1. Bhatnagar, P.L., Sahdev, P.L., Nuovo Cimento, 44, (1966), pp. 5-15

2. Carrus, P.A., Fox, P.A., Kopal, Z., Hoas, F. Ap. J., (1951), pp.113.

3. Grover R. and Hardy, J.W.: App. J.(1966),143.193,496,48

4. Hayes, W.O. The vorticity jump across a gas dynamics discontinuity. J. Fluid Mech, 2(1957), p.597-600.

5. Kanwal,R.P. Propagation of curved shocks in pseudo [1] stationary three dimensional gas flows. Illinois; J.Math, 2( 1958), p.129- 136.

6. Kanwal, R.P. Flows behind shock waves in conducting gases, Proc. Roy. Soc., 257 (1960), p.263268.

7. Kolobkov, N. Our Atmospherics Ocean Foreign Language Publishing, House Moscow,(1960),p.41.

8. Mitra, S. K. Upper atmosphere, Asiatic Society, Calcutta ( 1952).