IJCRR

IJCRR - 3(9), September, 2011

Pages: 109-113

Print Article   Download XML  Download PDF

FRACTAL DIMENSIONAL ANALYSIS OF TAMIL NADU RAINFALL

Author: R. Samuel Selvaraj, Raajalakshmi Aditya

Category: General Sciences

Abstract:In this paper, we use fractal dimensional analysis to investigate the Tamil Nadu rainfall dynamics. We analyze the time series data of Tamil Nadu rainfall (annual, south west and northeast) using Hurst exponent. We use the rescaled range (R/S) analysis to estimate the Hurst exponent for 110 years rainfall data. The result shows a varying degree of persistence over shorter and longer time scales corresponding to distinct values of the Hurst exponent. Our studies suggest that Hurst exponent(H) of the annual rainfall of Tamil Nadu is H=1 which predicts its periodic motion, for the southwest rainfall H=0.725 i.e. the time series covers more ?distance' than a random walk and is a case of persistent motion and for the northeast rainfall H=0.5 the time series is purely random. Further we analysis the fractal dimension for the Tamil Nadu rainfall; however, the fractal dimension of the annual and southwest rainfall of Tamil Nadu decreases to 1, the process becomes more and more predictable as it exhibits ?persistence? behavior. The northeast rainfall fractal dimension D for the time series is 1.5, which indicates that there is no correlation between amplitude changes corresponding to two successive time intervals. Therefore, no trend in amplitude can be discerned from the time series and hence the process is unpredictable.

Keywords: Fractal dimensional, Hurst exponent, Persistent, Random, Unpredictable.

Full Text:

INTRODUCTION

Tamil Nadu formerly known as Madras state is the only sub-division of the Indian union which receives more rainfall in the northeast monsoon (October-December) season than in the southwest monsoon (June- September) season. In the previous study based on 80 years rainfall data from 1891, it was found that the southeast and northeast monsoon seasons contribute about 34% and 47% respectively to the mean annual rainfall of this region1 .Thus the rainfall received in Tamil Nadu during the northeast monsoon season is of great economic value. Major agricultural operations are normally undertaken during that season. It has, however, been noted that the rainfall during northeast monsoon is highly variable2 . Therefore, if its behavior could be predicted in advance, it would go a long way toward helping the agricultural and industrial activities of the region. The southwest monsoon is a part of the equatorial westerly, and as such it is humid, unstable and of considerable vertical extent. On the other hand, the northeast monsoon is a part of the northeast trades and is comparatively dry, stable and of lesser vertical extent, about 1 to 2 Km. As a result of the fundamental differences in the origin and structure of these two monsoons, Tamil Nadu receives varying amounts of rainfall during the two rainy periods. Rao3 observed that in the same year, there is an indication that a good northeast monsoon rainfall over Tamil Nadu is generally associated with deficient or normal southwest monsoon rainfall and vice versa. Raj et al4 and Raj5 have identified a few upper air parameters that have predictive potential for northeast monsoon rainfall over Tamil Nadu and the southern region. The annual variability of Indian summer monsoon and northeast monsoon rainfall is determined by external forcings and nonlinear internal dynamics. Surface air temperature is one of the factors that influence monsoon variability. The distribution of surface air temperature over land and sea determines the locations of heat source and sink which in turn affect circulation pattern through thermal and latent heat energy exchange between atmosphere and the surface beneath. The Hurst exponent is a parameter that quantifies the persistent or anti-persistent (past trends tend to reverse in future) behavior of a time series. It determines whether the given time series is completely random or has some longterm memory. Fractal dimensional analysis of geophysical time series is a well established investigative tool for exploring the dynamics. This was initiated by Mandelbrot and Wallis in their series of seminal papers6-8 on this subject. This has been followed up by application of the techniques to various geophysical phenomena9-12 . Fractal dimensional analysis is particularly well suited to analyze the variability of a given time series.

Data

For the present study more than 110 years Tamil Nadu rainfall data is collected from the Indian meteorological department. The raw data of rainfall for the annual and seasonal months over Tamil Nadu are considered.

METHODOLOGY

To calculate the Hurst exponent, we estimate the dependence of the rescaled range on the time span w of observation. A time series of full length N is divided into a number of shorter time series of length w= N, N/2, N/4 ... The average rescaled range is then calculated for each value of n. For a (partial) time series of length n, the rescaled range is calculated as follows:

• Calculate the mean;
•  Create a mean-adjusted series;
•  Calculate the cumulative deviate series Z;
•  Compute the range R for Z;
•  Compute the standard deviation S for the data;
•  Calculate the rescaled range R/S and average over all the partial time series of length n.

The Hurst exponent is estimated by fitting the power law to the data. To estimate the value of the Hurst exponent, R/S is plotted against w on log-log axes. The slope of the linear regression gives the value of the Hurst exponent. If the Hurst exponent (H) is 0.5, then the time series is purely random. If H>0.5, the time series covers more ?distance‘ than a random walk, and is a case of persistent motion, while if H<0.5, the time series covers less ?distance‘ than a random walk it shows the anti- persistent behavior in time series. However, for periodic motion, the Hurst exponent is 1. The Hurst exponent is related to the fractal dimension D of the time series curve by the formula

D=2-H

If the fractal dimension D for the time series is 1.5, there is no correlation between amplitude changes corresponding to two successive time intervals. Therefore, no trend in amplitude can be discerned from the time series and hence the process is unpredictable. However, as fractal dimension decreases to 1, the process becomes more and more predictable as it exhibits ?persistence?. That is, the future trend is more likely to follow an established trend. As the fractal dimension increases from 1.5 to 2, the process exhibits ?anti-persistence?. That is, a decrease in the amplitude of the process is more likely to lead to an increase in the future. Hence, the predictability again increases.

RESULT

In order to understand the behavior of different dynamical systems we use the Hurst exponent. We consider 110 years data of southwest, northeast and annual rainfall of Tamil Nadu to calculate the Hurst exponent. Using the R/S method we compute the Hurst exponent as discussed in the methodology section, the Hurst exponent and fractal dimension are found to be

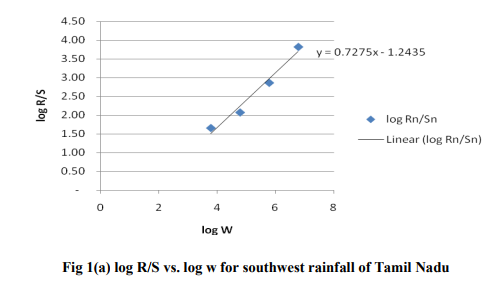
(i) for southwest rainfall H=0.725 and D=1.2

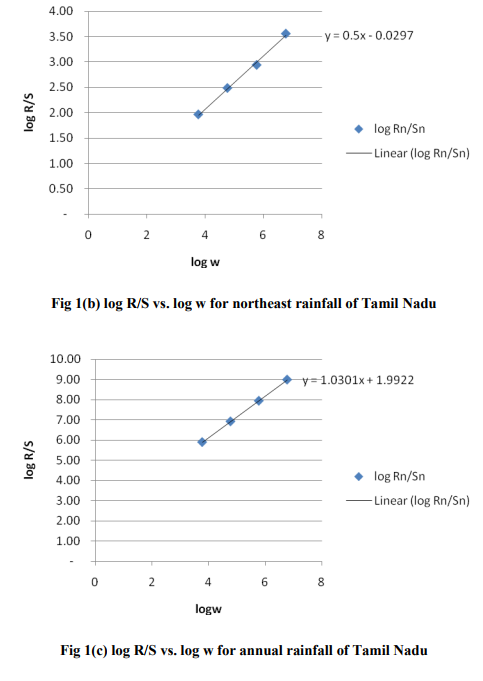
(ii) for northeast rainfall H=0.5 and D=1.5

(iii)for annual rainfall H=1 and D=1 In fig 1(a),(b)&(c) the slope of the linear regression gives the Hurst exponent for southwest, northeast and annual rainfall of Tamil Nadu.

CONCLUSION

Hurst exponent for southwest, northeast and annual rainfall of Tamil Nadu is estimated separately. Fractal dimension analysis is determined for all these three seasons using Hurst component. Hurst component of northeast is lower than both southwest and annual. Its Hurst exponent is 0.5 and fractal dimension D value is 1.5. It implies that northeast rainfall prediction is very complicated and is of unpredictable nature. In the cases of southwest Hurst exponent value is 0.725 and fractal dimension value is 1.2. It implies that further trend is more and more likely to follow an established trend. Tamil Nadu annual rainfall trend based on Hurst and fractal dimension is similar to southwest is periodic in nature. Both southwest and annual rainfall of Tamil Nadu is more or less similar and predictable.

References:

1. Dhar, O.N., Rakhecha, P.R. and Mandal, B.N., Some facts about Indian rainfall- A brief appraisal from hydrological consideration, Indian J. power river Val. Dev., (1981) 117-125.

2. Dhar, O.N., and Rakhecha, P.R. Foreshadowind northeast monsoon rainfall over Tamil Nadu, American meteorological society.,(1983) 109-111.

3. Rao, P. R. K., Rainfall of Madras state with special reference to Tamil Nadu and Rayalaseema, Indian meteor. Dept., (1953) 1-60.

4. Raj, Y.E.A., Sen, P.N and Jamadar, S.M., Outlook on northeast monsoon rainfall of Tamil Nadu, Mausam (1993) 19-22.

5. Raj, Y.E.A., A scheme for advanced prediction of northeast monsoon rainfall of Tamil Nadu, Mausam(1998) 247-254.

6. Mandelbrot, B.B., and Wallis, J.R., Some long-run properties of geophysical records, Water Resour Res (1969) 321

7. Mandelbrot, B.B., and Wallis, J.R., Noah, Joseph and operational hydrology, Water Resour Res (1968) 909

8. Mandelbrot, B.B., and Van Ness, J.W., Fractional Brownian motions, fractional noises and applications, SIAM Rev (1968) 422

9. Flugeman, Jr.R.H., and Snow, R.S., Fractal analysis of long-range paleoclimatic data: oxygen isotope record of pacific core, pure Appl Geophys (1989) 131

10. Hsui, A.T., Rust, K.A., and Kein, G.D., A fractal analysis of Quarternary, CenozoicMesozoic, and Late Pennsylvanian sea level changes, J Geophys Res (1993) 98

11. Turcotte, D.L., Fractals and chaos in geology and geophysics. New York, Cambridge University press (1992)

12. Theiler, J., Non linear forecasting measurements of multichannel EEG dynamics, Phys Rev(1986)2427